Введение понятия комплексного числа. Представление комплексного числа на плоскости

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы  , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:

.

(1)

В литературе часто мнимую единицу обозначают через  . Тогда комплексное число  можно представить в виде:

,

(2)

где   носит название действительной части или реальной части и обозначается  , а  носит название мнимой части и обозначается как  . Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (смотри рисунок 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.

Рисунок 1: Представление комплексного числа на плоскости

Комплексная плоскость   делится прямыми реальной части   (прямой действительных чисел) и прямой мнимых чисел  на четыре четверти. Любое комплексное число   ,будет представляться точкой на комплексной плоскости с координатами   и  . Если число не содержит мнимой части, то оно действительное и находится на прямой , а если число не содержит реальной части, то оно называется чисто мнимым и находится на оси  .

Операции над комплексными числами. Сложение комплексных чисел

Сумма двух комплексных числел   и   есть также комплексное число  :

.

(17)

Как следует из выражения (17) при сложении реальные и мнимые части комплексного числа также складываются.

На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рисунок 3).

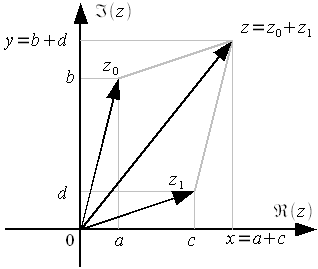Рисунок 3: Сложение комплексных чисел

Операции над комплексными числами. Вычитание комплексных чисел

Разность двух комплексных числел  и   есть также комплексное число  :

.

(18)

Как следует из выражения (18) при вычитании реальные и мнимые части комплексного числа также вычитаются.

На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов комплексных чисел по правилу параллелограмма (рисунок 4). На первом шаге из вектора   формиуется вектор   после чего вектор   складывается с вектором   по правилу параллелограмма.

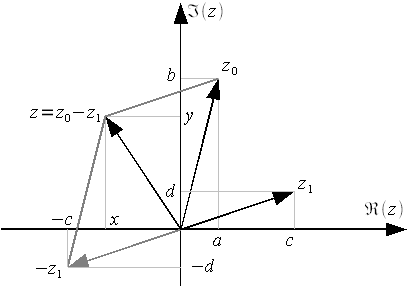Рисунок 4: Вычитание комплексных чисел

Операции над комплексными числами. Умножение комплексных чисел

Для того чтобы получить формулу для умножения комплексных числен необходимо перемножить два комплексных числа по правилу умножения многочленов:

(19)

Таким образом получили также комплексное число. Умножать в явном виде комплексные числа не очень удобно, гораздо проще если привести их по формуле Эйлера к показательной форме:

.

(20)

При перемножении в показательной форме модули комплексных числел перемножаются а фазы складываются. На векторной диаграмме это можно представить следующим образом (рисунок 5):

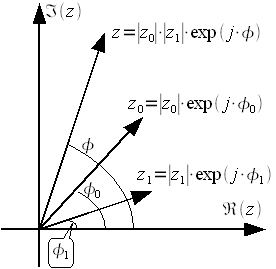Рисунок 5: Умножение комплексных чисел

При перемножении результирующий вектор поворачивается и его длина изменяется.

Исходя из выражения (15), умножение комплексного числа на чисто мнимое число приводит к повороту вектора на 90 градусов против часовой стрелки (к фазе   прибавляется 90 градусов). При этом из выражения (16) следует что умножение комплексного числа на -1 приводит повороту фазы на угол 180 градусов (вектор отражается относительно 0). Это очень важное замечание, так как емкости и индуктивности имеют чисто мнимые сопротивления и служат для поворота вектора комплесного сигнала, в то же время поворот фазы на 180 градусов позволяет сформировать фазоманипулированные сигналы.

Комплексно-сопряженные числаНеобходимо сделать еще одно замечание: числа   и   называются комплексно-сопряженными. При этом комплексно-сопряженное число обозначается чертой   Согласно выражениям (3) и (7) их модули равны, а фазы равны по модулю но имеют противоположные знаки:

.

(21)

Произведение согласно выражению (19) равно:

.

(22)

Таким образом произведение комплексно-сопряженных чисел есть действительное число равное квадрату модуля этих чисел. Векторное представление комплексно-сопряженных чисел представлено на рисунке 6.

Рисунок 6: Векторное представление комплексно-сопряженных чисел

Операции над комплексными числами. Деление комплексных чисел

Последняя операция которую осталось рассмотреть — операция деления комплексных чисел. Рассмотрим деление в показательной форме:

(23)

Таким образом при делении комплексных чисел их модули делятся а фазы вычитаются. При делении необходимо чтобы . Получим формулу для деления комплексных чисел в явной форме. Пусть

(24)

умножим и числитель и знаменатель дроби на число комплексно-сопряженное знаменателя:

.

(25)

Исходя из (22) в знаменателе дроби получим квадрат модуля знаменателя а числитель перемножим по правилу умножения комплексных чисел:

.

(26)

Поделив почленно реальную и мнимую часть числителя на знаменатель получим:

.

(27)

Выражение (27) - формула деления комплексных чисел в явной форме. Как можно заметить операции сложения и вычитания удобнее выполнять в явном виде, тогда как умножать и делить комплексные числа быстрее и легче в показательной форме.

Модуль и фаза комплексного числа

Если из начала координат комплексной плоскости к точке   восстановить вектор, то можно вычислить длину этого вектора как

.

(3)

При этом   — действительное число характеризующее длину вектора и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно оси   на некоторый угол  , называемый фазой. Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:

(4)

Тогда комплексное число можно представить в тригонометрической форме

.

(5)

Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа:

,

(6)

тогда

,

(7)

где   учитывает четверть комплексной плоскости в которой расположено число  :

.

(8)

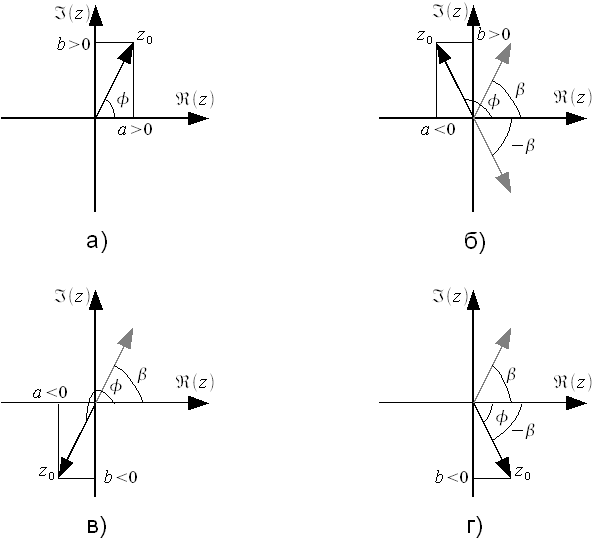Рисунок 2: Вычисление угла поворота вектора комплексного числа

Для того чтобы понять смысл функции   рассмотрим четыре варианта как это показано на рисунке 2.

Рисунок 2.а.  ,   и  , вектор в первой четверти плоскости. В этом случае   и  .

Рисунок 2.б.  ,   и   вектор во второй четверти плоскости. В этом случае  . Обозначим  , тогда  . угол   находится в четвертой четверти а угол   во второй. Для того чтобы получить угол   необходимо  , т.е. 

Рисунок 2.в.  ,   и   вектор в третьей четверти плоскости. В этом случае  . Обозначим  , тогда  . угол   находится в первой четверти а угол   в третьей. Для того чтобы получить угол   необходимо  , т.е.  .

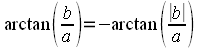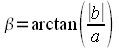Рисунок 2.г.   ,   и   вектор в четвертой четверти плоскости. В этом случае  . Обозначим  , тогда  . угол   находится как и угол   в четвертой четверти следовательно они равны, т.е.   и 

Функция которая позволяет получить угол   c учетом четверти комплексной плоскости в которой расположен вектор называется функция арктангенс-2 и обозначается  . Функция арктангенс-2 присутсвует во всех математических приложениях и может быть использована для расчета верного угла поворота вектора комплексного числа.

Показательная форма комплексного числа. Формула Эйлера

Существует также показательная форма комплексного числа связанная с тригонометрической по формуле Эйлера:

.

(9)

Данное соотношение легко доказать, если произвести разложение экспоненты в ряд Тейлора:

.

(10)

Представим ряд в виде суммы четных и нечетных членов последовательности:

.

(11)

Рассмотрим более подробно мнимую единицу в четной и нечетной степенях. Выражение (1) задало  , тогда , в свою очередь  . Таким образом можно рекурентно записать:

.

(12)

Построим аналогичным облразом рекурентное соотношение для нечетных степеней:  тогда  , в свою очередь  , получим:

.

(13)

Таким образом выражение (11) с учетом (12) и (13) принимает вид:

.

(14)

В выражении (14) первая сумма по четным степеням дает разложение в ряд Тейлора функции косинуса, а вторая сумма по нечетным степеням дает разложение в ряд Тейлора функции синуса. Таким образом, получено доказательство справедливости формулы Эйлера (9). Используя формулу Эйлера можно сделать ряд важных замечаний: Замечание 1:

.

(15)

Замечание 2:

.

(16)

Возведение комплексного числа в степень и извлечение корня из комплексного числа.

Определение 1. Из формулы для произведения комплексных чисел следует формула Муавра: если  , то

.

При возведении комплексного числа в натуральную степень модуль возводится в эту степень, а аргумент умножается на нее. Если   ,  то

,   .

Определение 2. Корнем  n-ой степени  (nÎN) из комплексного числа называется комплексное число,  n-ая степень которого равна подкоренному числу.

Выведем формулу для вычисления корня. Пусть  ,  . Тогда

.

По определению корня

                                                ,

                                                .

Чтобы выполнялось это равенство необходимо, чтобы

                                                ,    kÎZ;

                                                ,   , kÎZ.

Подставим данные значения в выражение для корня.

                                                .

Меняя     мы получим  n  различных значений корня из комплексного числа. Следовательно, корень  n–ой степени из действительного числа также имеет  n  комплексных значений, т.к. действительное число является частным случаем комплексного числа.

Некоторые элементарные функции.

Следующие функции (как однозначные, так и многозначные) называют основными элементарными функциями:

1. Дробно-рациональная функция

a) az+b, (а  0, а, b C) – линейная функция;

б) zⁿ , n N;– степенная функция с натуральным показателем;

в)  – дробно-линейная функция;

г) функция Жуковского  .

2. Показательная функция:

Наряду с введенным обозначением для показательной функции используют обозначение exp z.

Заметим, что на вещественной оси показательная функция комплексного переменного совпадает с показательной функцией действительного переменного. Непосредственная проверка убеждает, что на показательную функцию комплексного переменного переносится теорема сложения

Показательная функция комплексного переменного является периодической функцией с основным периодом 2pi, т. е.

.

3. Тригонометрические функции:

Для тригонометрических функций сохраняются теоремы сложения, а следовательно, и остальные формулы, справедливые для тригонометрических функций действительного переменного. Они являются периодическими функциями с теми же периодами, что и соответствующие тригонометрические функции действительного переменного.

Однако в случае комплексного переменного функции sinz, cosz ограниченными не являются.

4. Гиперболические функции:

 

5. Логарифмическая функция.

Логарифмическая функция Lnz, при z 0 определяется как обратная к показательной функции, причем

Так как показательная функция – периодическая с периодом 2pi, то логарифмическая функция является многозначной. В каждой точке z 0 она принимает бесконечно много значений.

Функция

где arg z – главное значение аргумента, называется главным значением логарифмической функции. Итак,

Известные правила о логарифме произведения и частного сохраняют свою силу и для многозначного логарифма, а именно: при z₁ и z₂, отличных от нуля, верны формулы

6. Общая степенная функция:

, a C.

Эта функция многозначная, её главное значение равно  .

При a=1/n, n  N получаем многозначную функцию – корень n-й степени из z:

Условия Коши — Римана, называемые также условиями Даламбера — Эйлера — соотношения, связывающие вещественную   и мнимую   части всякой дифференцируемой функции комплексного переменного  . В декартовых координатах

Для того чтобы функция  , определённая в некоторой области   комплексной плоскости, была дифференцируема в точке   как функция комплексного переменного  , необходимо и достаточно, чтобы её вещественная и мнимая части   и   были дифференцируемы в точке   как функции вещественных переменных   и   и чтобы, кроме того, в этой точке выполнялись условия Коши — Римана:

Компактная запись:

Если условия Коши — Римана выполнены, то производная   представима в любой из следующих форм:

[править]Доказательство

[править]1. Необходимость

По условию теоремы существует предел

,

не зависящий от способа стремления   к нулю. Положим   и рассмотрим выражение

.

Из существования предела комплексного выражения следует существование действительной и мнимой его частей. Поэтому в точке   существуют частные производные по x функций u(x,y) и v(x,y) и имеет место формула

Полагая  , находим

.

Сравнивая две последние формулы, убеждаемся в справедливости условий Коши-Римана.

[править]2. Достаточность

По определению дифференцируемости, приращения функций   и   в окрестности точки   могут быть записаны в виде

,

,

где функции   и   стремятся к нулю при  ,   быстрее, чем   и    ,  ,  . Составим теперь разностное соотношение  , где   и преобразуем его к виду

.

Заметим, что при стремлении   к нулю последнее слагаемое этой формулы стремится к нулю, а первые остаются неизменными. Поэтому существует предел  , что и доказывает дифференцируемость функции   в точке  .
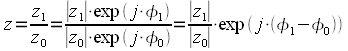
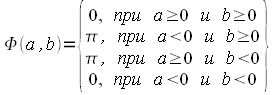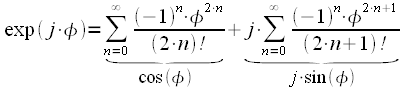