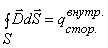- •32. Теорема Гауса для диэлектрического поля в диелектрике. Вектор Электрического смещения.
- •34. Спонтанная поляризация кристалических диэлектриков. Сегнетоэлектрики. Пироэлектрики. Пьезоэлектрики.
- •35. Свойства сегнетоэлектриков. Точка Кюри. Диэлектрический гистерезис.
- •36. Электростатическое поле внутри заряженного проводника и вблизи его поверхности. Проводники во внешнем электростатическом поле. Электроёмкость уединённого проводника.
- •37. Конденсаторы. Типы конденсаторов. Соединения конденсаторов. Ёмкость плоского конденсатора.
- •38. Энергия заряженных проводника и конденсатора. Энергия электрического поля. Объемная плотность энергии.
- •39. Электрический ток проводимости в металлах, его характеристики и условия существования. Сторонние силы. Электродвижущая сила и напряжение.
- •41. Работа и мощность тока. Закон Джоуля-Ленца в интегральной и дифференциальной формах.
- •42. Основы классической электронной теории электропроводности металлов. Удельная электропроводность. Подвижность носителей тока.
- •43. Закон Джоуля-Ленца, закон Виемана-Франца, закон Ома на основе классической теории электропроводимости.
- •44. Электрический ток в жидкостях и газах. Законы Фарадея для электролиза. Ионизация молекул газов. Электрический ток в газах. Газовые разряды. Электропроводность газов. Плазма.
- •45. Электрический ток в вакууме. Работа выхода электронов из металла. Контактная разность потенциалов. Термоэлектродвижущая сила. Эффекты Пельтье и Томсона.
- •46. Электрический ток в вакууме. Электронная эмиссия. Виды эмиссий и их применение. Формула Богуславского-Ленгмюра, формула Ричардсона. Вольтамперная характеристика вакуумного диода.
32. Теорема Гауса для диэлектрического поля в диелектрике. Вектор Электрического смещения.
Теорема
Гаусса для электростатического поля в
диэлектрике:
![]()
т.
е. поток вектора смещения электростатического
поля в диэлектрике сквозь произвольную
замкнутую поверхность равен алгебраической
сумме заключенных внутри этой поверхности
свободных электрических зарядов. В
такой форме теорема Гаусса справедлива
для электростатического поля как для
однородной и изотропной, и для неоднородной
и анизотропной сред. Для вакуума
![]()
![]() ,
тогда поток вектора напряженности Е
сквозь произвольную замкнутую поверхность
равен
,
тогда поток вектора напряженности Е
сквозь произвольную замкнутую поверхность
равен
![]() Так как источниками поля Е в среде
являются как свободные, так и связан
заряды, то теорему Гаусса для поля Е в
самом общем виде можно записать
Так как источниками поля Е в среде
являются как свободные, так и связан
заряды, то теорему Гаусса для поля Е в
самом общем виде можно записать
![]() где
где
![]() и
и
![]() — соответственно алгебраические суммы
свободных и связанных зарядов, охватываемых
замкнутой поверхностью S.
— соответственно алгебраические суммы
свободных и связанных зарядов, охватываемых
замкнутой поверхностью S.
Напряженность
электростатического поля,
![]() ,
зависит от свойств среды: в
однородной изотропной
среде напряженность поля Е
обратно
пропорциональна
,
зависит от свойств среды: в
однородной изотропной
среде напряженность поля Е
обратно
пропорциональна
![]() .
Вектор
напряженности
Е, переходя через границу диэлектриков,
претерпевает скачкообразное
изменение, создавая
тем самым неудобства при расчетах
электростатических полей. Поэтому
оказалось
необходимым
помимо вектора
напряженности
характеризовать
поле еще вектором
электрического смещения,
который для
электрически изотропной
среды, по определению, равен
.
Вектор
напряженности
Е, переходя через границу диэлектриков,
претерпевает скачкообразное
изменение, создавая
тем самым неудобства при расчетах
электростатических полей. Поэтому
оказалось
необходимым
помимо вектора
напряженности
характеризовать
поле еще вектором
электрического смещения,
который для
электрически изотропной
среды, по определению, равен
![]() .
Используя формулы
.
Используя формулы
![]() и
и
![]() ,
вектор электрического смещения можно
выразить как
,
вектор электрического смещения можно
выразить как
![]()
Единица электрического смещения — кулон на метр в квадрате (Кл/м2).
33. Условия на границе двух однородных изотопных диэлектриков. Вектор электрического смещения. Относительная диэлектрическая проницаемость.
|
Рассмотрим
поведение векторов ![]() на
границе раздела двух однородных
изотропных диэлектриков, диэлектрическая
проницаемость которых
на
границе раздела двух однородных
изотропных диэлектриков, диэлектрическая
проницаемость которых ![]() и
и ![]() ,
при отсутствии на границе свободных
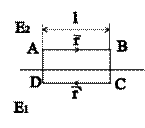
зарядов. Построим внутри границы раздела
диэлектриков 1 и 2 небольшой замкнутый
прямоугольный контур АВСДА длины l,
ориентировав его как показано на
рис. nобразует
правовинтовую систему с направлением
обхода по контуру. Условия на границе
получим с помощью теоремы Гаусса и
теоремы о циркуляции:
,
при отсутствии на границе свободных
зарядов. Построим внутри границы раздела
диэлектриков 1 и 2 небольшой замкнутый
прямоугольный контур АВСДА длины l,
ориентировав его как показано на
рис. nобразует
правовинтовую систему с направлением
обхода по контуру. Условия на границе
получим с помощью теоремы Гаусса и
теоремы о циркуляции:
|
|
|
|
|
|
Напряженность электростатического поля, , зависит от свойств среды: в однородной изотропной среде напряженность поля Е обратно пропорциональна . Вектор напряженности Е, переходя через границу диэлектриков, претерпевает скачкообразное изменение, создавая тем самым неудобства при расчетах электростатических полей. Поэтому оказалось необходимым помимо вектора напряженности характеризовать поле еще вектором электрического смещения, который для электрически изотропной среды, по определению, равен . Используя формулы и , вектор электрического смещения можно выразить как
Единица электрического смещения — кулон на метр в квадрате (Кл/м2).
Относительная диэлектрическая проницаемость среды ε — безразмерная физическая величина, характеризующая свойства изолирующей (диэлектрической) среды. Связана с эффектом поляризации диэлектриков под действием электрического поля (и с характеризующей этот эффект величиной диэлектрической восприимчивости среды). Величина ε показывает, во сколько раз сила взаимодействия двух электрических зарядов в среде меньше, чем в вакууме. Относительная диэлектрическая проницаемость воздуха и большинства других газов в нормальных условиях близка к единице (в силу их низкой плотности). Для большинства твёрдых или жидких диэлектриков относительная диэлектрическая проницаемость лежит в диапазоне от 2 до 8 (для статического поля). Диэлектрическая постоянная воды в статическом поле достаточно высока — около 80. Велики её значения для веществ с молекулами, обладающими большим электрическим диполем. Относительная диэлектрическая проницаемость сегнетоэлектриков составляет десятки и сотни тысяч.

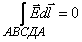 ,
,