25.26. Связь между напряжённостью и потенциалом электрического поля. Вычисление разности потенциалов по напряжению.

Э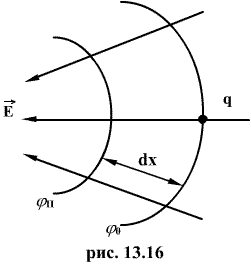 лектрическое поле характеризуется двумя физическими величинами: напряженностью и потенциалом. Пусть положительный заряд q перемещается силой электрического поля с эквипотенциальной поверхности, имеющей потенциал   , на близко расположенную эквипотенциальную поверхность, имеющую потенциал   (рис. 13.16).

Напряженность поля Е на всем малом пути dx можно считать постоянной. Тогда работа перемещения   С другой стороны   . Из этих уравнений получаем: .Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.

По известной напряженности поля будем искать разность потенциалов между двумя точками для различных случаев полей.  1. Поле равномерно заряженной бесконечной плоскости задается формулой: E=σ/(2ε₀), где σ — поверхностная плотность заряда. Разность потенциалов между точками, которые лежат на расстояниях x₁ и х₂ от плоскости, равна (используем формулу E_x = -∂φ/∂x)    2. Поле двух бесконечных параллельных разноименно заряженных плоскостей задается формулой: Е=σ/ε₀, где σ — поверхностная плотность заряда. Разность потенциалов между плоскостями, между которыми расстояние равно d (используем формулу E_x = -∂φ/∂x), равна   (1)  3. Поле равномерно заряженной сферической поверхности радиуса R с общим зарядом Q вне сферы (r>R) задается формулой: (4πε₀)^-1(Q/r²) разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра сферы (r₁>R, r₂>R, r₂>r₁), равна  (2)  Если положить r₁=r и r₂=∞, то потенциал поля вне сферической поверхности, согласно формуле (2), равен выражению    Внутри сферической поверхности потенциал везде одинаков и равен    4. Поле объемно заряженного шара радиуса R с общим зарядом Q вне шара (r>R) вычисляется, как известно, по формуле E = (4πε₀)^-1(Q/r²), поэтому разность потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ от центра шара (r₁>R, r₂>R, r₂>r₁), задается формулой (2). В любой точке, лежащей внутри шара на расстоянии r' от его центра (r'<R), напряженность определяется выражением (82.4): E = (4πε₀)^-1(Qr'/r³) Значит, разность потенциалов между двумя точками, которые расположены на расстояниях r₁' и r₂' от центра шара (r₁'<R, r₁'<R, r₂'>r₁' ), равна    5. Поле равномерно заряженного бесконечного цилиндра радиуса R, который заряжен с линейной плотностью τ, вне цилиндра (r>R) задается формулой: E = (2πε₀)^-1(τ/r) Значит, разность потенциалов между двумя точками, которые расположены на расстояниях r₁ и r₂ от оси заряженного цилиндра (r₁>R, r₂>R, r₂>r₁), равна

27. Работа по перемещении заряда в электрическом поле. Разность потенциалов. Потенциал электрического поля. Теорема о циркуляции вектора напряжённости эл. Поля.

Вычислим работу при перемещении электрического заряда в однородном электрическом поле с напряженностью   . Если перемещение заряда происходило по линии на пряженности поля на расстояние Ad = d₁-d₂ (рис. 110), то работа равна: , где d₁ и d₂ — расстояния от начальной и конечной точек до пластины В.

В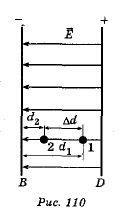 механике было показано, что при перемещении между двумя точками в гравитационном поле работа силы тяжести не зависит от траектории движения тела. Силы гравитационного и электростатического взаимодействия имеют одинаковую зависимость от расстояния, векторы сил направлены вдоль прямой, соединяющей взаимодействующие точечные тела. Отсюда следует, что и при перемещении заряда в электрическом поле из одной точки в другую работа сил электрического поля не зависит от траектории' его движения.

При изменении направления перемещения на 180° работа сил электрического поля, как и работа силы тяжести, изменяет знак на противоположный. Если при перемещении заряда q из точки В в точку С силы электрического поля совершили работу А, то при перемещении заряда q по тому же самому пути из точки С в точку В они совершают работу — А. Но так как работа не зависит от траектории, то и при перемещении по траектории СКВ тоже совершается работа — А. Отсюда следует, что при перемещении заряда сначала из точки В в точку С, а затем из точки С в точку В, т. е. по замкнутой траектории, суммарная работа сил электростатического поля оказывается равной нулю (рие.111).

Р абота сил электростатического поля при движении электрического заряда по любой замкнутой траектории равна нулю.

Поле, работа сил которого по любой замкнутой траектории равна нулю, называется потенциальным полем. Гравитационное и электростатическое поля являются потенциальными полями.

Разность потенциалов - скалярная величина, равная отношению работы электрического поля по перемещению положительного заряда из одной точки поля в другую точку к величине этого заряда. В СИ разность потенциалов измеряется в вольтах..

Электрическое поле, создаваемое системой неподвижных электрических зарядов обладает свойством потенциальности: работа электрического поля по перемещению постоянного точечного заряда вдоль замкнутого контура равна нулю.

Теор. циркуляции: Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд q₀, то сила, приложенная к заряду, совершает работу. Работа силы F на элементарном перемещении dl равна Так как , то

Работа при перемещении заряда q₀ из точки 1 в точку 2

(1)

Не зависит от траектории перемещения, а определяется только положениями начальной 1 и конечной 2 точек. Следовательно, электростатическое поле точечного заряда является потенциальным, а электростатические силы – консервативными, а электростатические силы – консервативными. Из формулы (1) следует, что работа, совершаемая при перемещении электрического заряда во внешнем электростатическом поле по любому замкнутому пути L, равна нулю, т.е. (2). Если в качестве заряда, переносимого в электростатическом поле, взять единичный точечный «+» заряд, то элементарная работа сил поля на пути dl равна Edl = E₁dl, где E₁=Ecosα – проекция вектора Е на направление элементарного перемещения. Тогда формула (2) можно записать в следующим виде (3). Интеграл называется циркуляцией вектора напряженности.