Доказательство.

Пусть, для определенности, f(a)<0, f(b)>0. Ситуация выглядит так:

Для доказательства теоремы снова используем метод деления отрезка пополам.

1. Деление отрезков пополам.

Разделим отрезок [a, b] пополам. Середина его будет точка  . Тогда возможны такие варианты:

а) . В этом случае, взяв  , теорему можно считать доказанной.

б)  . В этом случае для дальнейшего рассмотрения оставим отрезок  , который обозначим [a₁, b₁].

в)  В этом случае для дальнейшего рассмотрения оставим отрезок  , который обозначим [a₁, b₁].

Проделаем такую же процедуру с отрезком [a₁, b₁], получив отрезок [a₂, b₂], затем то же самое с отрезком [a₂, b₂], получив отрезок [a₃, b₃] и т.д. Заметим, что для дальнейшего рассмотрения все время оставляется тот отрезок, для которого f(a_n)<0 и f(b_n)>0.

2. Построение точки с.

В результате этой процедуры возможны два варианта.

А. На каком-то шаге n получится, что . В этом случае в качестве точки С следует взять   и теорема будет доказана.

Б. .

В этом случае мы получаем систему отрезков [a_n, b_n], для которой

а) [a,b] Й[a₁, b₁] Й [a₂, b₂] Й[a₃, b₃]…

б)

в)f(a_n)<0; f(b_n)>0

Но тогда, по лемме о вложенных отрезках, существует  . Используя непрерывность функции f(x), получим

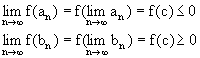
т.к. всегда было f(a_n)<0, f(b_n)>0. Сравнивая эти два неравенства получим, что f(c)=0, что и требовалось доказать.<

Вторая теорема Больцано-Коши. Пустьf(x) определена и непрерывна на отрезке <a,b> и  . Тогда  m<C<M  сО<a,b> f(c)=C.

Примечание. Символ < означает любой из двух символов – ( или [, а символ > - любой из двух символов - ) или ]. Таким образом, отрезок <a, b> означает любой из следующих отрезков – [a,b], (a,b], [a,b), или (a,b).

Доказательство.

Так как к супремуму и инфимуму можно подойти сколь угодно близко, то можно утверждать, что

x₁О<a, b> m<f(x₁)<C

x₂О<a, b> C<f(x₂)<M

Очевидно, что отрезок [x₁, x₂] М <a, b>.

Рассмотрим функцию j (x)=f(x)-C. Для нее имеем:

j (x₁)=f(x₁)-C<0; j (x₂)=f(x₂)-C>0.

Согласно первой теореме Больцано-Коши, сО<a, b>, такая, что j (с)=0. Но тогда эта же точка сО<a, b> и для нее j(с)=f(c)-C=0, т.е. f(c)=C. <

Первая теорема Вейерштрасса.

Пусть функция f(x) определена и непрерывна на замкнутом отрезке [a, b]. Тогда она ограничена на этом отрезке, т.е. существуют такие числа m и M, что  x принадлежащего [a,b] f(x) больше либо равно m и меньше либо равно M.

Доказательство.

Доказательство этой теоремы проведем методом от противного.

Предположим противное – пусть, например, функция f(x) неограничена сверху.

1. Построение последовательности. Мы предположили, что f(x) неограничена сверху на [a,b]. Это означает, что для любого числа А найдется такая точка xО[a,b], что f(x)>A.

Возьмем в качестве числа А числа 1, 2, 3, 4,… Тогда  , что f(x_n)>n.Мы получили, таким образом, некоторую последовательность {x_n}О[a,b] и удовлетворяющую свойству f(x_n)>n.

2. Выделение подпоследовательности. Так как последовательность {x_n} ограничена, то по лемме Больцано-Вейерштрасса из нее можно выделить сходящуюся последовательность {x_n}, т.е.  . В силу замкнутостиотрезка [a, b] точка cО [a,b]. (Отметим,что в этом месте используется ограничение теоремы – замкнутость [a,b]. Если бы, например, был (a,b), то с могла бы и не принадлежать (a,b)).

3. Сведение к противоречию.Т.к. согласно п.1  , то, переходя к пределу k®Ґполучим  т.е. f(c)=+Ґ, что противоречит условию теоремы, где сказано, что f(x) определена на отрезке [a,b],что означает, что f(c) должна иметь конечное значение. <

Вторая теорема Вейерштрасса.

Пусть функция f(x) определена и непрерывна на замкнутом отрезке[a,b]. Тогда существуют такие точки x₁, x₂ принадлежащие [a,b], что  , т.е. инфимум и супремум f(x) достигаются на [a,b].

Доказательство.

Докажем теорему только для супремума.

1. Построение последовательности. По первой теореме Вейерштрасса, f(x) ограничена сверху на [a,b],т.е. 

По свойствам супремума, к нему можно подойти сколь угодно близко. Поэтому  . Беря n=1,2,3,… получим последовательность {x₁, x₂, x₃,…}такую, что  .

2. Выделение подпоследовательности. Т.к.  n a£ x_n£ b, то по лемме Больцано-Вейерштрасса, из последовательности {x_n} можно выделить сходящуюся подпоследовательность   такую, что  , причем сО[a,b] в силу его замкнутости.

3. Достижение супремума. Для нашей подпоследовательности верно условие

.

4.Переходя к пределу k®Ґ получим

.

Но  , кроме того, в силу непрерывности f(x),  . В результате получим, что M£f(c)£ M, т.е. f(c)=M и супремум f(x) достигается в точке с.

35. Точки разрыва функции. Классификация точек разрыва

Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

 

Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

36. Три примера приводящие к понятию производной

Задача о скорости движения. Рассмотрим уравнение неравномерного прямолинейного движения S=¦(t), определенного на множестве (a,b). Зафиксируем последовательно два момента времени t₀ и t ₁ Î(a,b) и обозначим  D t =t₁ - t₀.

Средней скоростью движения, соответствующей некоторому промежутку времени t, называется отношение пройденного пути, за этот промежуток времени

Средняя скорость не характеризует движение в каждый момент времени. Для того чтобы найти скорость в данный момент t₀, необходимо уменьшить промежуток времени t=t₁-t₀. Чем меньше промежуток , тем меньше средняя скорость отличается от скорости в данный момент времени, т. е. от мгновенной, точное значение скорости   равно пределу   при , т. е.   

.                    

 

2.     Задача о касательной. Пусть на множестве (a, b) задана функция y=¦(x). Отметили в декартовой ee системе координат XOY график в виде кривой К x₀;

Возьмем две точки М₀ (¦(x₀)) и М₁(x₁;¦(x₁)) и проведем через них секущую М₀ М₁, ее угол наклона обозначим через a₁. Тогда, если точка М₁, двигаясь по кривой будет приближаться к точке М₀, положение секущей изменяется.

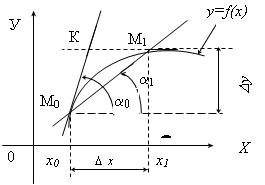
Рис. 2.17. К задаче о секущей

Когда точка М₁ совместиться с М₀, секущая превратиться в касательную. В этом случае  a₁=a₀, где a₀ - угол наклона касательной.

Из рисунка видно, что

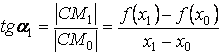
т.к. x₁-x₀=D x- это приращение аргумента, ¦(x₁)-¦(x₀)=D y - приращение функции, то

tga₁=                                                      

Осуществляя предельный переход, когда М₁ М₀

.

Учитывая (2-69), имеем

.              

Итак, тангенс угла наклона касательной  , равен пределу отношения приращения функции к приращению аргумента, когда последнее, равно нулю.

37. Определение производной

Это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.

38. Геометрический смысл производной

Геометрический смысл - тангенс угла касательной с осью иксов.

39. Экономическая интеграция производной

40. Основные свойства производной

Если u ( x ) ≡ const , то

u’ ( x ) ≡ 0 , du ≡ 0.

Если u ( x ) и v ( x ) - дифференцируемые функции в точке x0 , то:

( c u )’ = c u’ , d ( c u ) = c du , ( c – const );

( u ± v )’ = u’ ± v’ , d ( u ± v ) = du ± dv ;

( u v )’ = u’ v + u v’ , d ( u v ) = v du + u dv ;

Производная сложной функции. Рассмотрим сложную функцию, аргумент которой также является функцией:

h ( x ) = g ( f ( x ) ).

Если функция f имеет производную в точке x0, а функция g имеет производную в точке f ( x0 ), то сложная функция h также имеет производную в точке x0 , вычисляемую по формуле:

h’ ( x0 ) = g’ ( f ( x0 ) ) · f’ ( x0 ) .