Шпаргалка по Мат. Анализу

1. Декартовая система координат (ДСК)

Системой координат называется совокупность одной, двух, трех или более пересекающихся координатных осей, точки, в которой эти оси пересекаются, – начала координат – и единичных отрезков на каждой из осей. Каждая точка в системе координат определяется упорядоченным набором нескольких чисел – координат. В конкретной невырожденной координатной системе каждой точке соответствует один и только один набор координат.

2. Декартовая прямоугольная система координат (ДПСК)

Если в качестве координатных осей берутся прямые, перпендикулярные друг другу, то система координат называется прямоугольной (или ортогональной). Прямоугольная система координат, в которой единицы измерения по всем осям равны друг другу, называется ортонормированной (декартовой) системой координат

3. Полярная система координат

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

4. Деление направленного отрезка (вектора) в заданном отношении

1. Если x₁ и y₁ - координаты точки A, а x₂ и y₂ - координаты точки B, то координаты x и y точки C, делящей отрезок AB в отношении  , определяются по формулам

Если  , то точка C(x, y) делит отрезок AB пополам, и тогда координаты x и y середины отрезка AB определяются по формулам

2. Площадь треугольника по известным координатам его вершин A(x₁, y₁), B(x₂, y₂), C(x₃, y₃) вычисляется по формуле

Полученное с помощью этой формулы число следует взять по абсолютной величине.

3. Площадь многоугольника с вершинами A(x₁, y₁), B(x₂, y₂), C(x₃, y₃), ..., F(x_n, y_n) равна

Выражение вида   равно x₁y₂ - x₂y₁ и называется определителем второго порядка.

5. Виды задания прямой на плоскости – векторное и общее уравнение, векторно-параметрическое, параметрическое, каноническое, уравнение прямой проходящей через две заданные точки, уравнение прямой в «отрезках», с угловым коэффициентом, нормированное (нормальное) уравнение прямой на плоскости

Общее уравнение прямой

где   – некоторые числа. При этом коэффициенты   одновременно не равны нулю, так как уравнение теряет смысл.

 Векторно-параметрическое уравнение прямой 

где   - фиксированная точка, лежащая на прямой;   - направляющий вектор.

     В координатах (параметрические уравнения):

Параметрическое уравнение прямой

Могут быть записаны в виде:

где   — производный параметр,   — координаты   и   направляющего вектора прямой. При этом

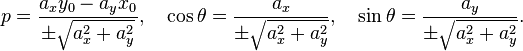
 Канонические уравнения прямой 

     Уравнения прямой по двум точкам 

Уравнение прямой в отрезках

Уравнение прямой линии, пересекающей ось   в точке   и ось   в точке  :

В этом виде невозможно представить прямую, проходящую через начало координат.

Угловой коэффициент

Уравнение прямой линии, пересекающей ось   в точке   и образующей угол   с положительным направлением оси  :

Коэффициент   называется угловым коэффициентом прямой. В этом виде невозможно представить прямую, параллельную оси 

Нормальное уравнение прямой

где   — длина перпендикуляра, опущенного на прямую из начала координат, а   — угол (измеренный в положительном направлении) между положительным направлением оси   и направлением этого перпендикуляра. Если  , то прямая проходит через начало координат, а угол   задаёт угол наклона прямой.

6. Взаимное расположение прямых на плоскости

Две прямые могут:

1) совпадать;

2) быть параллельными:  ;

3) или пересекаться в единственной точке:  .

Две прямые совпадают, тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, то есть, существует такое число «лямбда», что выполняются равенства 

Две прямые параллельны тогда и только тогда, когда их коэффициенты при переменных   пропорциональны:  , но  .

Две прямые пересекаются, тогда и только тогда, когда их коэффициенты при переменных   НЕ пропорциональны, то есть НЕ существует такого значения «лямбда», чтобы выполнялись равенства 

7. Расстояние от точки до прямой на плоскости. Площадь треугольника

Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.

Если задано уравнение прямой на плоскости Ax + By + C = 0, то расстояние от точки M(Mx, My) до прямой можно найти используя следующую формулу

d =	|A·Mx+ B·My+ C|
	(A2 + B2)1/2

Пояснения к формулам:  a, b, c - длины сторон треугольника, площадь которого мы хотим найти  r - радиус вписанной окружности  R - радиус описанной окружности  h - высота треугольника, опущенная на сторону  p - полупериметр треугольника, 1/2 суммы его сторон 

8. Преобразование ДПСК на плоскости. Обе ДПСК – правые

Т.е. новые ДПСК не меняют ориентацию.

Получается в результате преобразования старой ДПСК поворотом на угол фи против часовой стрелки и параллельным переносом на вектор ОО’

9. Преобразование ДПСК на плоскости. ДПСК имеют разные ориентации

Получаются параллельным переносом и осевой симметрией. Т.е. новая система координат будет – левая. Обе ДПСК тогда имеют разные ориентации

10. Алгебраические линии

Алгебраическим полиномом n-й степениотносительно двух переменных x и y называется конечная сумма слогаемых вида

, где i,k = N i+k≤n и существует С_ik≠0 при i+k=n

Если уравнение в ДПСК имеет вид F(x,y) = 0, где F(x,y) – алгебраический полином n-го порядно относительно х и у, то а называется алгебраической линией n-го порядка.

11. Эллипс

Эллипс – геометрическое множество точек плоскости, сумма расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, большая, чем расстояние между фокусами 2c:  причем 

12. Гипербола

Гипербола – геометрическое множество точек плоскости, модуль разности расстояний от которых до двух точек и , называемых фокусами, есть величина постоянная 2a, меньшая, чем расстояние между фокусами 2c:  причем 

13. Парабола

   Парабола – множество точек плоскости, равноудаленных от данной точки F, называемо фокусом, и данной прямой, называемой директрисой:  .

14. Линии (кривые) второго порядка. 9 канонических уравнений

  Алгебраической кривой второго порядка называется кривая Г, уравнение которой в декартовой системе координат имеет вид:

 

Аx² + 2Вxy + Сy² + 2Dx + 2Еy + F = 0,

 

где не все коэффициенты А, В и С равны одновременно нулю.

 

Если кривая Г невырожденная, то для неё найдется такая декартова прямоугольная система координат, в которой уравнение этой кривой примет один из следующих трех видов (каноническое уравнение):

 

 - эллипс,

 

 - гипербола,

 

px  - парабола.

 

 

где не все коэффициенты А, В и С равны одновременно нулю. 

Эллипс.

Каноническое уравнение эллипса:   

Гипербола.

Каноническое уравнение гиперболы:   

Парабола.

Каноническое уравнение параболы:   

Пара пересекающихся прямых.

Уравнение:   

Пара параллельных прямых.

Уравнение:   

Пара совпадающих прямых.

Уравнение:   

Мнимый эллипс.

Уравнение мнимого эллипса:  

Пара пересекающихся снимых прямых.

Уравнение: 

Пара параллельных мнимых прямых.

Уравнение:   

15. Понятие множества. Операции над множествами (алгебра множеств)

Элементы множества − это то, из чего это множество состоит

Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается

Если любой элемент множества A является элементом другого множества B, то говорят, что A есть подмножество множества B, и пишут: A   B

1. Коммутативность.

A  B=B  A A  B=B  A

2. Ассоциативность.

(A  B)  C=A  (B  C) (A  B)  C= A  (B  C)

3. Дистрибутивность.

(A  B)  C = (A  C)  (B  C) (A  B)  C= (A  C)  (B  C)

A  A=A, A  A=A A  = A, A 

4. Законы де Моргана (законы двойственности).

1) A  B= A  B  2) A  B= A  B

16. Эквивалентность множеств

Множества, между которыми можно установить взаимно однозначное соответствие, называются эквивалентными или равномощными. Два конечных множества эквивалентны тогда и только тогда, когда в них одинаковое количество элементов.

17. Множество вещественных чисел

Множество вещественных чисел обозначается R и часто называется вещественной прямой

18. Комплексные числа. Действия над комплексными числами

Комплексным числом   называется число вида  , где   и   – действительные числа,   – так называемая мнимая единица. Число   называется действительной частью ( )комплексного числа  , число   называется мнимой частью ( ) комплексного числа  .

• Сложение

• Вычитание

• Умножение

• Деление

19. Понятие отображения, функции

Отображение (матем.) множества А в множество В, соответствие, в силу которого каждому элементу х множества А соответствует определённый элемент у = f (x) множества В, называют образом элемента х (элемент х называют прообразом элемента у).  Отображением множества E в множество F, или функцией, определенной на E со значениями в F, называется правило, или закон f, который каждому элементу ставит в соответствие определенный элемент .

Функция — математическое понятие, отражающее связь между элементами множеств

20. Понятие последовательности

Пределом последовательности элементов метрического пространства называют элемент того же пространства, который обладает свойством «притягивать» элементы заданной последовательности. Пределом последовательности элементов топологического пространства является такая точка, каждая окрестность которой содержит все элементы последовательности, начиная с некоторого номера.

Пусть дано топологическое пространство    и последовательность   Тогда, если существует элемент   такой, что

,

где   — открытое множество, содержащее  , то он называется пределом последовательности  . Если пространство является метрическим, то предел можно определить с помощью метрики: если существует элемент   такой, что

,

где   — метрика, то   называется пределом  .

21. Суперпозиция отображений. Обратное отображение

Пусть   и  . Поскольку  , то отображение g каждому элементу   относит определенный элемент  .

Таким образом, каждому   посредством правила   поставлен в соответствие элемент

Тем самым определено новое отображение (или новая функция), которое назовем композицией отображений, или суперпозицией отображений, или сложным отображением.

 Пусть   - биективное отображение и F = {y}. В силу биективности f каждому   соответствует единичный образ x, который обозначим через f ^-1(y), и такой, что f(x) = y. Таким образом, определено отображение  , которое называется обратным отображению f, или обратной функцией функции f.

Очевидно, отображение f обратно отображению f ^-1. Поэтому отображения f и  f ¹ называют взаимно обратными. Для них справедливы соотношения

22. Понятие предела числовой последовательности. Сходящиеся и расходящиеся последовательности

Число   называется пределом числовой последовательности  , если последовательность   является бесконечно малой, т. е. все её элементы, начиная с некоторого, по модулю меньше любого заранее взятого положительного числа.

В случае, если у числовой последовательности существует предел в виде вещественного числа  , её называют сходящейся к этому числу. В противном случае, последовательность называют расходящейся. Если к тому же она неограниченна, то её предел полагают равным бесконечности.

Кроме того, если все элементы неограниченной последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равенплюс бесконечности.

Если же элементы неограниченной последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.

Числовая последовательность, имеющая предел, называется сходящейся, а не имеющая предела — расходящейся.

1,2,3,4,5 – расходящаяся

1, 4\3, 6\4, 2n\n+1 - сходящаяся

23. Основные свойства сходящихся последовательностей

Сходящаяся последовательность имеет только один предел.

Доказательство. Предположим, что два вещественных числа а и b являются пределами сходящейся последовательности {xn}. xn=a+an и xn=b+bn, где {an} и {bn} - некоторые бесконечно малые последовательности. Получим an−bn=b−a . Последовательность {an−bn} является бесконечно малой, а в силу равенства an−bn=b−a все элементы этой бесконечно малой последовательности равны одному и тому же вещественному числуb−a . Число b−a равно нулю, т. е. b=a. Теорема доказана.

Всякая сходящаяся последовательность является ограниченной.

Доказательство. Пусть {xn} - сходящаяся последовательность и a ее предел. Фиксируем некоторое положительное число ε и по нему номер N такой, что ∣xn−a∣<ε при n≥N или, a−ε<xn<a+ε при n≥N . Обозначим через A наибольшее из следующих (N+1) чисел: ∣a−ε∣,∣a+ε∣,∣ ∣ x1∣ ∣ ,∣ ∣ x2∣ ∣ ,...,∣ ∣ хN−1∣ ∣ . Тогда, очевидно, ∣xn∣≤A для всех номеров n, а это и доказывает ограниченность последовательности {xn}. Теорема доказана.

Сумма сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен сумме пределов последовательностей {xn} и {yn}.

Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам а и b соответственно. Тогда в силу того что xn=a+an будут справедливы соотношения

xn=a+an,yn=b+bn, (6),

в которых anи bn представляют собой элементы некоторых бесконечно малых последовательностей {an} и {bn}. Из (6) вытекает, что(xn+yn)−(a−b)=an+bn . (7)

Т.к. сумма {an+bn} двух бесконечно малых последовательностей {an} и {bn} представляет собой бесконечно малую последовательность, то из соотношения (7) вытекает в силу определения, что последовательность {xn+yn} сходится и вещественное число a+b является ее пределом. Теорема доказана.

Разность сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен разности пределов последовательностей {xn} и {yn}

Доказательство этой теоремы аналогично доказательству Теоремы 3, только вместо соотношения (7) мы получим соотношение (xn−yn)−(a−b)=an−bn .

Произведение сходящихся последовательностей {xn} и {yn} представляет собой сходящуюся последовательность, предел которой равен произведению пределов последовательностей {xn} и {yn}.

Доказательство. Предположим, что последовательности {xn} и {yn}сходятся к пределам a и b соответственно. Тогда для элементов этих последовательностей справедливы (6), перемножая которые, мы получим

xn·yn=a·b+abn+ban+an·bn или, xnyn−a·b=abn+ban+an·bn (8)

Лемма 1. Если последовательность {yn} сходится к отличному от нуля пределу b, то, начиная с некоторого номера, определено частное {1yn} последовательностей {\{}1{\}} и {yn}, которое представляет собой ограниченную последовательность.

Частное двух сходящихся последовательностей {xn} и {yn}, предел второй из которых отличен от нуля, определено, начиная с некоторого номера, и представляет собой сходящуюся последовательность, предел которой равен частному пределов последовательностей {xn} и {yn}.

Доказательство. Предположим, что последовательности {xn} и {yn} сходятся к пределам a и b соответственно. В силу леммы 1 найдется номер N такой, что при n>N элементы yn нe обращаются в нуль, определена последовательность {1yn} и эта последовательность является ограниченной. Начиная с номера N, мы и будем

рассматривать частное {ynxn} . В силу определения достаточно доказать, что последовательность {ynxn−ba} является бесконечно малой. Будем исходить из тождества ynxn−ba=yn·bxn·b−yn·a (9)

Т.к. для элементов xn и yn справедливы (6), то

n·b−yn·a=(a+an)·bn−(b+bn)·an=anb−bna

Подставляя (10) в (9), получим ynxn−ba=1yn(an−babn) (11)

Остается доказать, что в правой части (11) стоит элемент бесконечно малой последовательности, но это сразу вытекает из того, что последовательность {1yn} (в силу леммы 1) является ограниченной, а последовательность {an−babn} (как разность двух бесконечно малых) является бесконечно малой последовательностью. Теорема доказана.

24. Число е

e — математическая константа, основание натурального логарифма, трансцендентное число.

e ≈ 2,7182

25. Предел функции на бесконечности

Предел функции на бесконечности в математическом анализе описывает поведение значения данной функции, когда её аргумент становится бесконечно большим по модулю.

• Пусть задана числовая функция с неограниченной сверху областью определения, то есть 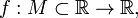  и   Тогда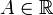  наывается пределом функции   при  стремящемся к бесконечности, если

Пишут:

• Аналогично пусть   и 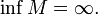  Число   называется пределом функции   при   стремящемся к минус бесконечности, если

Пишут:

26. Предел функции. Арифметические свойства предела функции

Пусть EМ R и a – предельная точка множества E.

Будем говорить, что a –предельная точка для множества E, если любая окрестность точки a содержит бесконечное подмножество множества E.

Пусть f:E  R. Приведем несколько формулировок определения предела функции.

последовательности fxng и fyng схо-

дятся. Тогда

limn!1(xn + yn) = limn!1 xn + limn!1 yn ;

limn!1(xn yn) = limn!1 xn limn!1 yn ;

limn!1(xn yn) = limn!1 xn limn!1 yn ;

27. Односторонние пределы. Теорема о существовании предела функции

Односторонний предел в математическом анализе — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левосторонним пределом и правосторонним пределом

28. Бесконечно малые и бесконечно большие функции

Бесконечно малая— числовая функция или последовательность, которая стремится к нулю.

Последовательность   называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  .

Бесконечно большая— числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция  , неограниченная с обеих сторон, не является бесконечно большой при  .

Последовательность   называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки  , если  .

Функция называется бесконечно большой на бесконечности, если   либо  .