5. Падение плоской волны на границу реального проводника. Приближенные граничные условия Леонтовича. Мощность потерь в хорошо проводящей среде.

Когда среда 2 - неидеальный металл , электрическое поле в нем не равно нулю. Относительная комплексная диэлектрическая проницаемость

.

При значениях из (5.1) следует, что угол преломления можно считать равным нулю при любых , т.е. преломленная волна в металлоподобной среде нормальна границе сред (приближение Леонтовича). На границе металла существует отличная от нуля . Несмотря на малость этой величины, она обеспечивает поток вектора Пойнтинга вглубь металла, определяющий тепловые потери. Мощность тепловых потерь определяется как

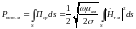
Полагая, что совпадает по величине с 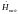на поверхности идеального металла при 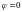, в соответствии с (5.5), .

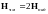6. Падение плоской волны с параллельной и перпендикулярной поляризацией на границу раздела с идеальным проводником. Характеристики направляемой волны. Волны е- и н-типа.

Для нормальных составляющих справедливы соотношения:

(2.7)

при отсутствии поверхностных электрических зарядов.

Если на границе раздела сред равномерно распределен электрический поверхностный заряд с удельной плотностью , то

(2.8)

Для тангенциальных составляющих электрического поля справедливо

(2.9)

Если вторая среда – идеальный проводник (с бесконечной проводимостью), то E_1τ=0 и на границе существует только нормальная составляющая электрического поля.

Для магнитной составляющей в общем случае

, (2.10)

На поверхности идеального проводника вводится понятие поверхностного электрического тока , измеряемого в А/м:

, (2.11)

численно равного нормальной составляющей вектора поля на границе и ориентированного перпендикулярно ему.

Н-тип волны, или ТЕ-волна (поперечно электрическая). Такие волны содержат и продольные и поперечные составляющие магнитного Н-поля, электрическое поле имеет только перпендикулярную составляющую ().

Е-тип волны, или ТН-волна (поперечно магнитная). Такие волны содержат одновременно и продольные и поперечные составляющие электрического поля, магнитное поле имеет только поперечную составляющую ().

Тема 4. Волноводы.

1. Прямоугольный волновод. Связь продольных и поперечных составляющих поля в волноводе (без вывода формул связи). Критическая длина волны.

Конструкция прямоугольного металлического волновода (ПМВ) представляет собой трубу прямоугольного поперечного сечения с внутренними размерами a x b (рис. 6.1). Все основные свойства и расчетные соотношения (6.1) – (6.5) для плоского волновода

Рис.6.1. Металлический волновод прямоугольного поперечного сечения

Волны электрического типа Е_mn:

У волны Е-типа низшим типом является Е₁₁.

Волны магнитного типа Н_mn:

У волны Н-типа низшим типом является Н_10.

Критическая длина волны — это наибольшая длина волны, которая может распространяться в волноводе для данного типа колебаний.