Тема 2. Плоские электромагнитные волны.

1. Уравнения Гельмгольца для векторов поля и его решение.

Волновой процесс – явление переноса энергии поля в пространстве и во времени. Для гармонически меняющегося поля (например, Е или Н) - описывается уравнением Гельмгольца:

Частное решение уравнения Гельмгольца для ЭМ поля, изменяющегося во времени по гармоническому закону в неограниченном пространстве

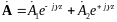, 2 волны, бегущие навстречу друг другу

где

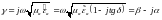
- комплексная постоянная распространения,

- фазовая постоянная, - постоянная затухания.

2. Плоская однородная линейно поляризованная электромагнитная волна. Характеристики плоской волны. Связь характеристик плоской электромагнитной волны с параметрами среды. Фазовая и групповая скорость. Длина волны.

Волна – это колебательные движения непрерывной среды.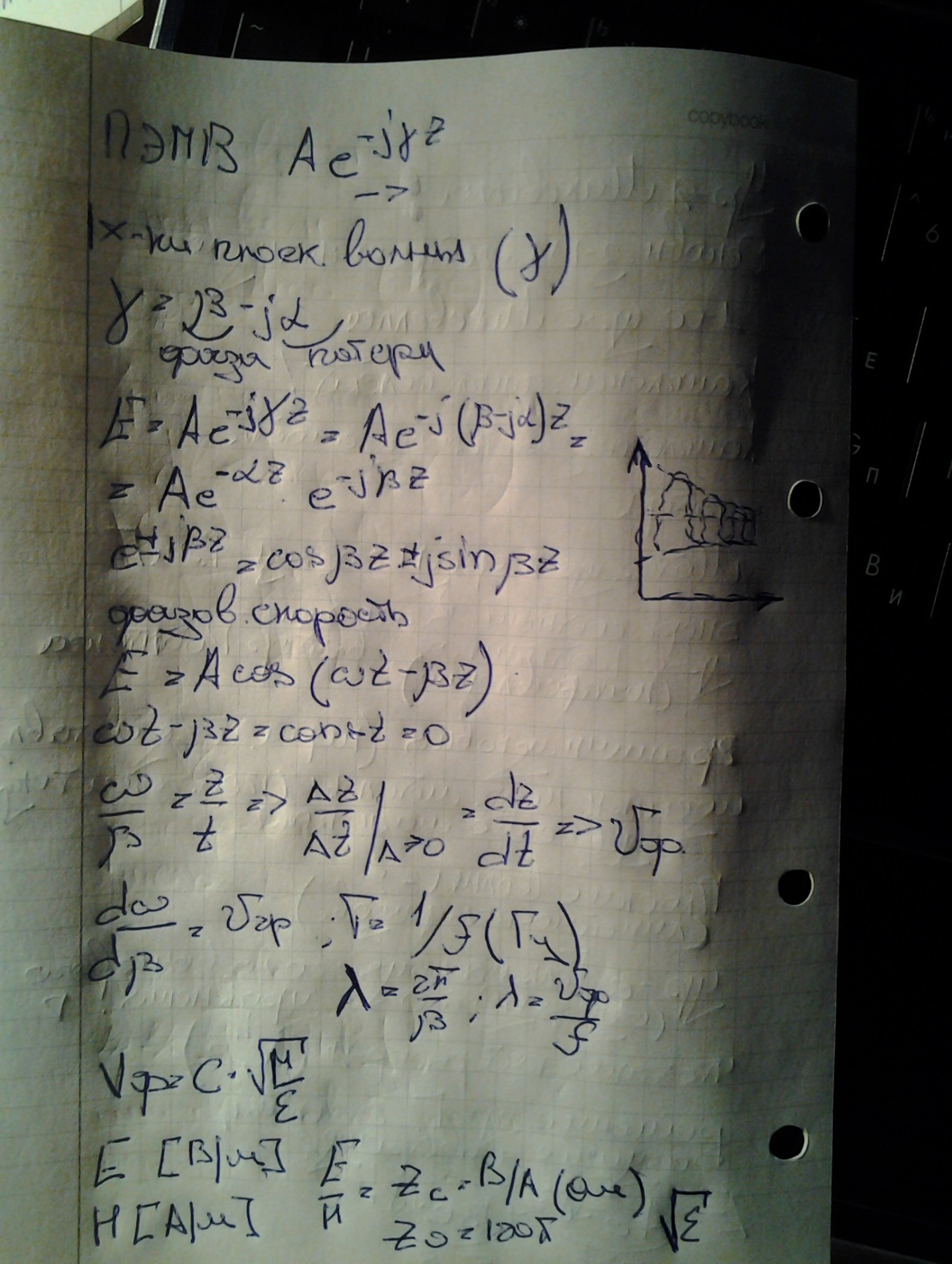

Тема 3. Отражение и преломление плоских волн.

1. Падение плоских электромагнитных волн на границу раздела двух сред. Законы Снеллиуса. Понятие коэффициентов отражения и преломления.

Рис.5.1 Падение плоской волны на границу двух сред

под произвольным углом

Явления на границе раздела рассматриваются в предположении, что обе среды без потерь (tgδ=0), а граница раздела – плоская. Тогда соотношения углов падения, отражения и преломления определяются законами Снеллиуса:

Коэффициенты отражения и преломления определяются соотношениями:

при параллельной поляризации

;

при перпендикулярной поляризации

,……… ……..

где , - характеристические сопротивления сред,

Если волна падает нормально к границе раздела , значения R и T от поляризации не зависят.

2. Определение коэффициентов отражения и преломления в случае перпендикулярной поляризации. Графики зависимости этих коэффициентов от угла падения.

,

3. Определение коэффициентов отражения и преломления в случае параллельной поляризации. Графики зависимости коэффициентов от угла падения.

;

4. Явление полного преломления. Угол Брюстера. Полное внутреннее отражение (пво). Коэффициент отражения при пво. Распределение поля поверхностной волны.

При определенном сочетании параметров в средах без потерь отраженная волна может отсутствовать. Угол падения, при котором падающая волна полностью проникает во вторую среду ( ), называется углом Брюстера . Для случая немагнитных диэлектриков ( ) и при ε₂> ε₁ явление имеет место при параллельной поляризации. При этом

В случае, когда волна падает из воздуха ( =1), .

Если > , то, согласно (5.2), > . Угол падения, при котором = /2, называется углом полного внутреннего отражения , поскольку вся энергия падающей волны отражается от границы раздела коэффициент отражения по модулю тождественно равен единице. При > |R|=1, меняется только фаза. При этом плоскость постоянных фаз волны распространяется вдоль границы раздела сред (вдоль оси x), а плоскость постоянных амплитуд – вдоль оси z. В среде 1 поле вдоль оси z меняется по гармоническому закону – волна становится неоднородной, а в среде 2 - экспоненциально спадает при удалении от границы раздела по закону

,

где - мнимая часть угла преломления при > .