20. Объясните геометрический смысл введения дополнительного ограничения в методе Гомори. Приведите пример.

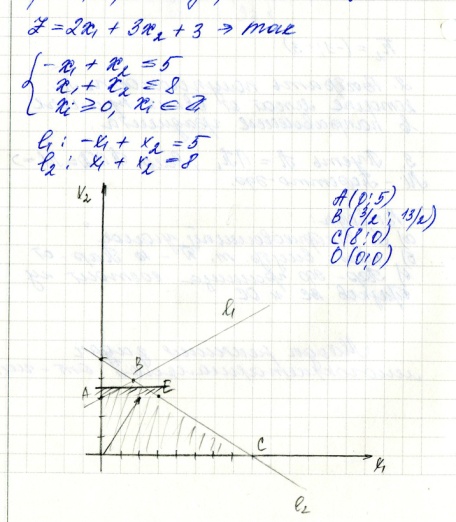
Х₃+Х₄ >=1

-Х₁+Х₂+Х₃ = 5 => Х₃=5+Х₁-Х₂

Х₁+Х₂+Х₄=8 => Х₄=8-Х₁-Х₂

5 + Х₁-Х₂+8-Х₁-Х₂>=1

2Х₂<=12

X₂<=6

Неравенство Х₂<=6 отсекает от доп. области часть, которая содержит целочисленное решение => метод сечений.

21. Общая постановка задач многокритериальной оптимизации. Примеры задач с экономическим содержанием.

Пример: агентство (10чел.) получило заказ на размещ. рекл. на ТВ и радио.

	Радио	ТВ
Аудитория(млн.чел.)	4	8
Стоимость (тыс.руб.)	8	24
Кол-во зан-х агентов	1	2

Сколько мин.рекл.времени должно купить рекл.агентсво на радио и ТВ, если по контр-ту запрещ. испол. бол. 6 мин. на радио. Ауд. д.б. макс, а издержки – миним.

Пусть х – кол-во мин. на радио, у – на ТВ.

{█(х≤6@х+у≤10; х,у≥0)┤ f_1=4х+8у→max f_2=8х+24у→min f_(2*)=-8х-24у→max

22. Что называется оценкой допустимого решения задачи многокритериальной оптимизации? Как определяется отношение строгого предпочтения на множестве допустимых решений D? Приведите примеры несравнимых элементов из D .

Оценкой допустимого решения задачи наз. вектор f.

f(x)= (f_1 (x),…,f_n (x) ) Пусть “<” – строгое предпочтение на множ-ве Д, т.е., если х,у принадлеж. Д, то х<у: f(x) <=f(y). Т.е., f_i (x)≤f_i (y),i=1,…,n.  Замечание: эл-ы мн-ва Д не всегда сравнимы. Пример:  x_(=(1;1) ) y_(=(3/2;1/2) ) f(x)=(f_1 (x),f_2 (x) )=(12;-32) f(y)=(f_1 (y),f_2 (y) )=(10;-24)

23. Дайте определения доминирования по Парето. Приведите примеры. Эффективное (недоминируемое) решение.

В сл. несравнимых реш-й, выбор лучшего из них зависит не только от усл-я задач, но и от предпочт-й лица, приним-го реш-я.

Отнош-е строго “<” предпочтение можно ослабить. Пусть х,у прин-т Д.

Говорят, что х доминир-т над у (х>у), если х не хуже у по всем критер-м и сторого бол. хотя бы по одному их них, т.е. 1) f_i (x)≥f_i (y),для ∀ i=1,…,n. 2) 〖∃ j: f〗_i (x)≥f_j (y) Домин-е по Парето. Пример: А(0;5): f(A)=(f_1 (A),f_2 (A) )=(40;-120) В(6;2): f(B)=(f_1 (B),f_2 (B) )=(40;-96)

Допустим. реш-е х принадл. Д наз. эффект-м.

24. Дайте определение Парето-эффективной границы и приведите пример ее построения.

Множ-во всех парето-опт. реш-й наз. парет-опт. границей.

1. проведем через точку М линии уровня на кажд. из целевых функций (f_1,f_2,…,f_n )

f_1: n ̅_1=(4;2) f_2: n ̅_2=(-8;-24)

2. выбрать полуплоскости , кот. лежат от своих прямых в напр. вектора градиента.

3. Если пересеч. П и Д = М (пересеч. по ед. точке), то М оптим. по Парето.

(Нарисовать)

25. Основные методы решения задач многокритериальной оптимизации.

1)Выбор решения из Парето-эффективных границ пред-ся ЛПР (лицу принимающего решение)

2)Производится сужение Парето-эффективной границы при помощи дополнительной информации по критериям и свойства эффективных решений: а) метод обобщенного критерия; б) метод приоритетов.