14. Влияние фактора времени и температуры на механические характеристики материа­ле. Понятие о ползучести, релаксации и длительной прочности.

Влияние температуры на свойства металлов. При повышен­ных температурах модули упругости и предел текучести, как прави­ло, уменьшаются. Коэффициент Пуассона зависит от температуры незначительно.

Для описания зависимости модулей упругости от температуры предлагается использовать формулу, введенную Дж. Ф. Беллом после экспериментального исследования более 500 металлов и сплавов:

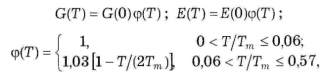(1)

где, Т - температура материала (в градусах Кельвина); G(T),Е(Т)- модуль сдвига и модуль Юнга при температуре Т;

G(0), Е(0) - те же модули при так называемой нулевой температуре;

φ(Т) - линейная функция температуры;

Т_m - температура плавления материала.

Значения G(0), E(0) легко получить, используя соотношения (1), если известны величины соответствующих модулей при ком­натной температуре и температура плавления материала.

Зависимость предела текучести от температуры эксперимен­тально исследовалась многими механиками. Один из способов ее описания предложил Н. А. Махутов ':

σ_yo - предел текучести при температуре Т_о;

σ_yo = σ_y(T₀) ;

k - экспериментальная константа материала.

Например, для сплава Д16Т:

T_m=933K, k=301 K^-1, G(o)=0.308*10^11 Па

E(0)=0.829*10^11 Па

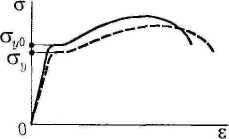
Изменение диаграммы растяжения об­разца в поле повышенных температур схематично показано на рисунке 2. Диаграмма наклоняется вправо (за счет уменьшения модуля Юнга), становится ниже (уменьшается предел текучести) и вытягивается вдоль оси деформаций.

Ползучестью, или крипом, называется процесс изменения деформаций со временем при постоянном напряжении. Соответст­вующие графики называются кривыми ползучести

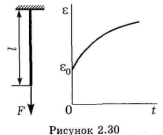
На рисунке 3схематически пока­заны условия испытания и кривая пол­зучести. Верхний конец образца закреп­ляется, к нижнему прикладывается на­грузка. Ведется наблюдение за изменени­ем длины в расчетной части образца и строится кривая изменения деформации s от времени t. Деформация увеличивается от своего начального значения go, ко­торое соответствует «мгновенно» прило­женной нагрузке F.

Явление напряжения в образце при постоянной деформации наъывается релаксацией. Предположим, что мгновенно растянули так, что расчетная длина l₀ стала равной l (рисунок 3). Для этого потребовалась сила F₁. Образец закрепили в растянутом состоянии на некоторое время. Затем его освободили от закрепления и вновь приосвободили от закрепления и вновь приложили нагрузку, чтобы расчетную часть образца растянуть до величины L Оказывается, потребовалась нагрузка F₂, меньшая первоначальной £\. Поэтому говорят, что на­пряжение, требующееся для поддержания постоянной деформации, падает, уменьшается, релаксирует.

18.Расчёты на прочность и жёсткость при растяжении-сжатии.

Расчет на прочность. При расчетах на прочность (по первому предельному состоянию) в конструкции ограничиваются наибольшие напряжения. Условие прочности имеет вид

σ_мах≤ Ry_c,

где γ _с - коэффициент условий работы (в большинстве случаев y_с < 1)..

Расчет на жесткость. В случае расчета на жесткость (по второ­му предельному состоянию) в системе ограничивают максимальные перемещения δ_мах. Условие жесткости имеет вид

δ _мах≤ [δ],

где [δ] - допускаемое значение перемещений.

Замечание. Метод расчета по предельным состояниям позво­ляет производить расчеты конструкций как в предположении упру­гой работы материала, так и с учетом пластических деформаций (по диаграмме Прандтля).

19.Коэффициент запаса прочности. Технико-экономические факторы, влияющие на коэффициент запаса.

Вопрос о выборе коэффициента запаса прочности решается с учётом имеющегося опыта эксплуатации машин. В последнее время один общий коэффициент запаса прочности К , разделяют на ряд составляющих коэффициентов запаса, каждый из которых отражает влияние на прочность деталей какого-либо фактора или группы факторов. Такое разделение коэф-та позволяет лучше учесть многообразие конкретных условий работы деталей машин и проектировать их с большей надёжностью.

В справочнике машиностроителя используется три частных коэффициента:

К₁-коэф-т учитывающий неточность в определении нагрузок и напряжений.

К₂-коэф-т учитывающий неоднородность материала, его повышенную чувствительность механической обработки.

К₃-коэф-т условий работы, учитывающий также степень ответственности детали.

На коэф-т запаса влияют : факторы снижающие прочность материала детали(перегрузки, неоднородность материала).