
- •Наука о сопротивлении материалов. Основные гипотезы и допущения сопротивления материалов.
- •Внешние силы и их классификация: поверхностные и объемные, статические и динамические.
- •Основные объекты, изучаемые в сопротивлении материалов: брус (стержень), пластина, оболочка, массивное тело. Понятие о расчетной схеме конструкции.
- •Главный вектор и главный момент внутренних сил в сечении. Внутренние силы в поперечном сечении бруса.
- •Напряжения. Их связь с внутренними силовыми факторами.
- •Перемещения и деформации.
- •Центральное растяжение-сжатие прямого стержня. Продольные силы, их связь с нагрузкой.
- •Перемещения и деформации. (6)
- •Напряжения в поперечных сечениях бруса.
- •Продольные и поперечные деформации бруса. Закон Гука при растяжении и сжатии.
- •11 Удлинение (укорочение) бруса постоянного поперечного сечения. Жесткость при растяжении и сжатии. Перемещения поперечных сечений бруса.
- •12 Напряжения на косых площадках. Теорема парности касательных напряжении nри растяжении-сжатии.
- •13 Потенциальная энергия деформации при растяжении-сжатии.
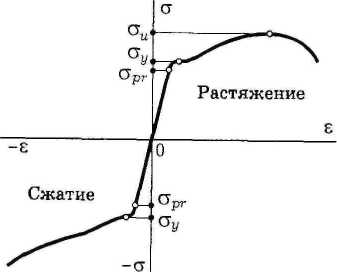
- •Диаграмма растяжения пластических материалов. Основные механические характеристики материалов
- •Диаграмма сжатия для пластических материалов. Разгрузка и повторное нагружение.Гипотеза упругой разгрузки. Эффект Баушингера (наклеп).
- •Диаграммы растяжения и сжатия хрупких материалов и основные механические характеристики. Особенности разрушения хрупких материалов.
- •Влияние фактора времени и температуры на механические характеристики материале. Понятие о ползучести, релаксации и длительной прочности.
- •20.Расчёт конструкций по методу предельных состояний. Допускаемые напряжения, их выбор.
- •21.Понятие о методе расчёта статически неопределимых систем по предельному состоянию, экономическая эффективность.
- •22.Деформация чистого сдвига .Закон Гука при сдвиге.
- •26. Задачи при расчете стержня на кручение:
- •27.Потенциальная энергия деформации
- •28 .Кручение стержня некруглого поперечного сечения
- •31. Главные оси инерции. Главные моменты инерции. Вычисление моментов инерции сложных сечений. Радиусы инерции.
- •32.Чистый изгиб прямого бруса в главной плоскости. Закон Гука при изгибе.
- •33.Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.
- •34. Нормальные напряжения при чистом изгибе. Жесткость при изгибе
- •35.Прямой поперечный изгиб. Распространение выводов чистого изгиба на поперечный изгиб.
- •36.Касательные напряжения при изгибе брусьев сплошных сечений(ф-ла Журавского). Распределение касательных напряжений по сечениям прямоугольного и двутаврового профиля.
- •37.Нормальные и касательные напряжения в сплошных и слоистых (листовой пакет) брусьях, прогибы в этих брусьях. Влияние касат.-х напряжений на эксплуатационные характеристики(гибкость, прогиб) рессоры.
- •38.Касательные напряжения в тонкостенных стержнях. Центр изгиба
- •39.Потенциальная энергия деформации при изгибе
- •40.Расчёты на прочность при изгибе.
- •41.Случаи, в которых необходима проверка прочности балок по касательным напряжениям.
- •42. Рациональные сечения при изгибе.
- •43.Понятие о кривом брусе большой и малой кривизны. З-н Гука для бруса большой кривизны. Связь изгибающего момента и нормальных напряжений для кривого бруса. Эпюра нормальных напряжений.
- •44.Определение нулевой линии для некоторых видов поперечных сечений бруса большой кривизны.
- •45. Дифференциальное уравнение упругой линии балки. Его непосредственное интегрирование. Граничные условия.
- •47. Теорема о взаимности работ(теорема Бетти)
- •47. Теорема о взаимности перемещений (теорема Максвелла)
- •Определение перемещений методом интеграла Мора.
- •Правило Верещагина.
- •51. Формула Cимпсона, Мюллера-Бреслау.
- •52. Основы метода сил.
- •53. Матрица податливости. Механический смысл коэффициентов матрицы податливости, приемы вычисления коэффициентов.
- •54. Основы метода перемещений. Канонические уравнения метода перемещений.
- •55. Матрица жесткости. Механический смысл коэффициентов матрицы жесткости, приемы вычисления коэффициентов.
- •56 Общий случай напряженного состояния в точке. Понятие о тензоре напряжений. Закон парности касательных напряжений.
- •57. Напряжения на произвольно ориентированной (косой) площадке.
- •59 Вековое уравнение. Инварианты тензора напряжений. Классификация видов ндс по инвариантам тензора напряжений.
- •6 0) Напряжения на октаэдрических площадках.
- •61.Площадки с наибольшими касательными напряжениями
- •62..Главное значение тензора напряжений.Положение главныхплощадок при плоском ндс
- •63 Площадки с наибольшими касательными напряжениями (площадки сдвига), их положение при плоском ндс.
- •64 Разложение тензора напряжений на шаровой тензор и девиатор напряжений. Интенсивность напряжений
- •65.Понятия о деформированном состоянии в точке
- •66 Перемещение, относительные деформации и сдвиги
- •69. Обобщенный закон Гука.
- •70. Объемная деформация. Закон Гука для объемной деформации.
- •71.Полная потенциальная энергия деформации. Потенциальная энергия изменения объема и формы.
- •72. Классификация напряженных состояний. Понятие об эквивалентном напряжении.
- •73.Сложное сопротивление: косой изгиб. Определение напряжений и положения нейтральной линии при косом изгибе.
- •74.Сложное сопротивление: внецентральное растяжение сжатие. Определение напряжений и положений нейтральной линии при внецентральном растяжении –сжатии. Ядро сечения.
Диаграмма сжатия для пластических материалов. Разгрузка и повторное нагружение.Гипотеза упругой разгрузки. Эффект Баушингера (наклеп).
Диаграммы сжатия пластичных материалов. Испытание на сжатие пластичных материалов, несмотря на простоту, менее распространено, чем испытание на растяжение. Объясняется это прежде всего тем, что в упругой стадии и при малом развитии пластических деформаций диаграмма сжатия таких материалов полностью повторяет диаграмму растяжения (рисунок 1) и не дает никаких новых механических характеристик. Пределы пропорциональности, упругости и текучести имеют те же значения. Их и модуль Юнга для малоуглеродистой стали при растяжении и сжатии можно считать совпадающими.
Различия начинаются после предела текучести. Площадка текучести менее выражена, чем при растяжении. Сжатие сопровождается увеличением площади поперечного сечения образца, поэтому испытание требует постоянно возрастающей нагрузки.
Исследуемый образец (цилиндр) сначала принимает бочкообразную форму (рисунок 2), а затем, не разрушаясь, расплющивается. Дальнейшее испытание ограничивается возможностями испытательной машины.
Следовательно, определить предел прочности невозможно. В расчетной практике предел прочности на сжатие σuс условно принимают таким же, как и на растяжение σut:
 Увеличение
предела текучести материала при
растяжении приводит,
как правило, к уменьшению его при сжатии.
Подобные изменения механических
характеристик материала после
пластического деформирования
носит название эффекта
Баушингера .
Увеличение
предела текучести материала при
растяжении приводит,
как правило, к уменьшению его при сжатии.
Подобные изменения механических
характеристик материала после
пластического деформирования
носит название эффекта
Баушингера .
Диаграммы растяжения и сжатия хрупких материалов и основные механические характеристики. Особенности разрушения хрупких материалов.
Д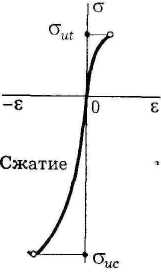 иаграммы
сжатия
хрупких
материалов.
Для
хрупких материалов, таких, как
чугун, бетон и другие каменные материалы,
испытание на сжатие является основным.
Их образцы доводят до разрушения, а
предел
прочности устанавливают, как при
растяжении:
иаграммы
сжатия
хрупких
материалов.
Для
хрупких материалов, таких, как
чугун, бетон и другие каменные материалы,
испытание на сжатие является основным.
Их образцы доводят до разрушения, а
предел
прочности устанавливают, как при
растяжении:
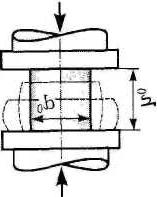
Диаграмма сжатия хрупкого материала по виду напоминает диаграмму растяжения (рисунок 1), но сопротивление сжатию в несколько раз больше, чем сопротивление растяжению (σuc » σut). Разрушение при сжатии происходит обычно путем сдвига одной части образца относительной другой.
Рисунок 1
П лоскость
сдвига в чугунном образце наклонена
примерно под углом 45° к оси (рисунок
2, а), что объясняется действующими на
ней максимальными касательными
напряжениями.
Характер разрушения бетонного кубика
представлен на рисунке 2, б..
лоскость
сдвига в чугунном образце наклонена
примерно под углом 45° к оси (рисунок
2, а), что объясняется действующими на
ней максимальными касательными
напряжениями.
Характер разрушения бетонного кубика
представлен на рисунке 2, б..
Если уменьшить влияние сил трения путем смазки, то образец разрушится при меньшей нагрузке, характер разрушения при этом будет другим (рисунок 2., б). Для большинства материалов стандартным является испытание без смазки
Диаграммы растяжения хрупких материалов. Диаграмма растяжения хрупких материалов показана на рисунке 3. Здесь отклонение от закона Гука наблюдается в начальной стадии нагру-жения, и модуль Юнга не является постоянной величиной.
Однако в пределах тех невысоких растягивающих напряжений, при которых хрупкие материалы работают в конструкциях, криволинейность диаграммы незначительна и ею пренебрегают, заменяя кривую секущей и считая
Е = tg α= const.
Хрупкие материалы плохо сопротивляются
Рисунок 3
растяжению. Предел прочности 𝜎и при растяжении невелик. Опасность хрупкого разрушения заключается в том, что оно происходит быстро, почти внезапно, без образования шейки.
