14. Диаграмма растяжения пластических материалов. Основные механические характе­ристики материалов

Диаграммы растяжения пластичных материалов, не имеющие площадки текучести. Ярко выраженная площадка текучести присуща только диаграммам сталей с содержанием углерода 0,1-0,3 %, лату­ни и некоторых видов бронзы. Большинство пластичных материалов

Рисунок

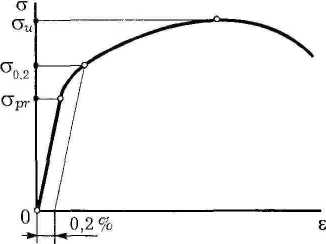
не имеет площадки текучести на диаграмме растяжения (рисунок ). Это, например, алюминие­вые сплавы, стали с содержанием углерода менее 0,1 % или 0,3...0,5 %, легированные стали. После упругой работы диаграмма растяжения таких материалов получает закругление и затем сразу переходит в кривую, харак­теризующую стадию упрочнения. Таким образом, указанные мате­риалы ведут себя как пластич­ные, т. е. разрушаются после раз­вития больших остаточных деформаций.

Для пластичных материалов, не имеющих площадки текучести, вводится условное понятие технического предела текучести (в отличие от физического, охарактеризованного выше). За него при­нимают напряжение, при котором остаточная деформация достигает примерно того же значения, что и при наличии площадки текучести. В качестве условного предела текучести обычно берется σ_0,2, т. е. напряжение, соответствующее пластической деформации ε_pl = 0,2 %.

Механическими характеристиками конструкционных материалов называются величины, характеризующие их прочность, пластичность, твердость и т. д., а также модули упругости и коэф­фициент Пуассона.

Характеристики прочности. Основными механическими ха­рактеристиками прочности пластичных материалов являются предел текучести 𝜎_u и предел прочности 𝜎_и при растяжении, хрупких - пре­дел прочности при сжатии 𝜎_ис.

Характеристики пластичности. При испытании на растяжение образцов из пластичных материалов, кроме характеристик проч­ности, определяют также характеристики пластичности:

■ относительное остаточное удлинение при разрыве

где l_o - первоначальная длина образца;

l₁- суммарная длина двух частей разорванного образца;

■ относительное остаточное сужение при разрыве

где А_о - первоначальная площадь поперечного сечения образца;

А₁- площадь поперечного сечения в наиболее тонком месте шейки после разрыва.

Энергетические характеристики. В п. 2.6 было показано, что площадь диаграммы F-AI в пределах упругих деформаций выражает работу силы F в тех же пределах. Очевидно, площадь всей диаграм­мы растяжения или сжатия характеризует полную работу, затра­ченную на разрушение образца.

Пластич. материал Хрупк. материал

И з сопоставления диаграмм

на рисунке видно, что для разрушения пластичного материала необходимо затратить значи­тельно больше работы, чем для разрушения хрупкого. Следователь­но, если конструкция предназначена для восприятия динамических нагрузок, которые сопровождаются выделением большого количества энергии, предпочтение должно быть отдано пластичному материалу.

Хрупкие материалы легко и быстро разрушаются от динамиче­ских, а особенно от ударных воз­действий из-за своей недостаточной энергоемкости. С другой стороны, при статическом нагружении хруп­кие материалы вполне работоспо­собны и надежны.

У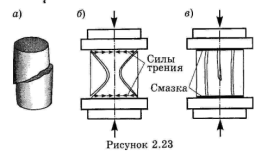 дарной вязкостью называют величину, характеризую­щую способность материала сопротивляться действию ударных на­грузок. Меру сопротивления удару определяют на специальных коп­рах, на которых при помощи маятника разрушаются образцы. Удар­ную вязкость а определяют как отношение работы W, затраченной на разрушение образца, к площади его поперечного сечения:

а = W/A.

Твердость.- Твердостью называют способность материала сопротивляться механическому проникновению в него другого тела. Наиболее широкое распространение получили испытания твердости по Бринеллю и по Роквеллу .

При испытании по Бринеллю стальной шарик, имеющий твер­дость стекла (из закаленной хромистой стали), диаметром 10 мм вдавливается определенной силой F в испытуемый материал (для стали F = 30 кН). После этого измеряют диаметр полученного отпе­чатка и находят величину А площади сферической поверхности, ос­тавшейся в материале в результате его пластической деформации. Величина давления шарика F/A дает меру твердости материала и называется числом Бринелля НВ = F /А.

П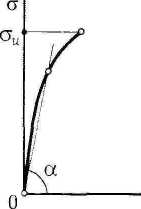 ри испытании по Роквеллу в материал вдавливают острый алмазный наконечник в виде конуса. Число Роквелла HR оп­ределяется, как и НВ. В справочной литературе приведены таблицы, устанавливающие зависимость между твердостью по Бринеллю и Ро­квеллу.

Испытания материалов должны проводиться по методикам, стро­го регламентированным ГОСТами и ведомственными нормами. Ме­ханические характеристики материалов зависят от многих факторов, в числе которых можно назвать, например, химический состав и технологию получения материалов, виды термической обработки и обработки резанием, условия эксплуатации и др.