12 Напряжения на косых площадках. Теорема парности касательных напряжении nри растяжении-сжатии.

Напряжения на наклонных площадках

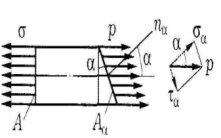
Рассмотрим растянутый призматический стержень. Выделим из него элемент (рисунок 1,а) двумя сечениями: левое сечение пер­пендикулярно оси стержня, правое - наклонно, его нормаль п_а со­ставляет с осью стержня угол α.

Определим напряжения на полученных площадках. Напряженное состояние рассматри­ваемого стержня при растяжении однородно, поэтому во всех точках.

Уравнение равновесия элемента стержня следующее

-σА + рА_а = 0,

где А - площадь поперечного сечения;

А_а - площадь наклонного сечения, А_α = A/cosα. Отсюда полное напряжение на наклонной площадке р = σ cos α

Раскладывая его на нормальную σ_а и касательную _а составляю­щие, получаем: σ_α =pcosα, α =psinα

или σ_α=σcos ² α, (1) α=1/2σsin ² α. (2)

Формулы (1), (2) определяют нормальные и касательные напряжения на наклонных площадках

при растяжении-сжатии.

Следствия. Проанализируем некоторые частные случаи при­менения полученных соотношений:

• если положить α = 0, то из формул (1), (2) получим

напряжения в поперечном сечении стержня: σ_а = σ; _а = 0;

• в продольных сечениях (а = 90°) напряжения σ_а = _а = 0, т. е. продольные волокна при растяжении-сжатии друг на друга надавят;

• в сечении под углом 45° к поперечному сечению σ_а = _а = σ/2; при этом касательные напряжения достигают максимума _α = t_max = /2.

Касательные напряжения на двух взаимно перпендикулярных площадках.

β= α+ 90°

Пусть нормаль к од­ной из площадок n_а составляет с осевой линией угол α. Тогда у дру­гой площадки нормаль n_β составит угол β= α+ 90° (рисунок 2). Касательные напряжения на первой площадке определяются формулой (2). На второй площадке

| _β|=|1/2σsin2β|=|1/2σsin(2α+180^o)|= |1/2σsin2α| =|τ_α|

Таким образом, касательные напряжения на двух взаимно пер­пендикулярных площадках растянутого стержня равны между собой по модулю.

13 Потенциальная энергия деформации при растяжении-сжатии.

Упругое тело является аккумулятором энергии, затраченной на его деформирование. Это свойство широко используется в различных амортизирующих устройствах (рессорах, пружинах и др.).

При нагружении тела внешние силы совершают работу W, кото­рая, с одной стороны, идет на сообщение скорости массе тела, т. е. переходит в кинетическую энергию К, с другой - накапливается в виде потенциальной энергии деформации U. Таким образом, уравне­ние энергетического баланса имеет вид:

W = K + U.

Если нагрузка прикладывается статически, т. е. возрастает от нуля до конечного значения настолько медленно, что можно пренеб­речь скоростью деформации и силами инерции, то К = 0. Работа внешних сил полностью преобразуется в потенциальную энергию:

W = U.

На рисунке а показан растянутый стержень, который в ре­зультате статического действия силы F удлиняется на Δl.

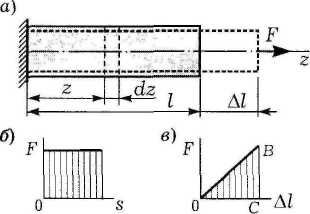
В теоретической механике ра­бота определяется произведением постоянной силы F на путь s, пройденный точкой ее приложе­ния по направлению действия си­лы: W=Fs. Эта работа выражает­ся площадью прямоугольника, построенного в системе координат Fиs (рисунок б).

В нашем случае сила F не ос­тается постоянной на пути Δl. При соблюдении закона Гука она линейно возрастает от нуля до своего конечного значения (рисунок в). Поэтому работа (а значит, и потенциальная энергия) чис­ленно равна площади треугольника ОВС:

W=U=1/2FΔl (1)

Это выражение справедливо для любой линейно-деформируемой системы, причем не только при растяжении-сжатии, но и при дру­гих видах деформации. Оно известно под названием теоремы Клапейрона. Если материал идеально упругий, но сама система не является линейно деформируемой, то теорема неприменима.

Переходя от внешней силы F к равной ей внутренней силе N, с учетом зависимости Δl = Nl/(EA) получаем:

U=N²l/2EA (2)

Формула применима только к брусьям (или отдельным участкам) постоянного сечения в случае постоянной продольной си­лы. При переменных по длине оси бруса значениях продольной силы N(z) и жесткости EA(z) потенциальная энергия деформации опреде­ляется суммированием по участкам или интегрированием вдоль оси стержня по всей его длинеl:

(3)

Отметим, что энергетические соотношения (2), (3) используют­ся при определении перемещений в стержневых системах .