
- •Наука о сопротивлении материалов. Основные гипотезы и допущения сопротивления материалов.
- •Внешние силы и их классификация: поверхностные и объемные, статические и динамические.
- •Основные объекты, изучаемые в сопротивлении материалов: брус (стержень), пластина, оболочка, массивное тело. Понятие о расчетной схеме конструкции.
- •Главный вектор и главный момент внутренних сил в сечении. Внутренние силы в поперечном сечении бруса.
- •Напряжения. Их связь с внутренними силовыми факторами.
- •Перемещения и деформации.
- •Центральное растяжение-сжатие прямого стержня. Продольные силы, их связь с нагрузкой.
- •Перемещения и деформации. (6)
- •Напряжения в поперечных сечениях бруса.
- •Продольные и поперечные деформации бруса. Закон Гука при растяжении и сжатии.
- •11 Удлинение (укорочение) бруса постоянного поперечного сечения. Жесткость при растяжении и сжатии. Перемещения поперечных сечений бруса.
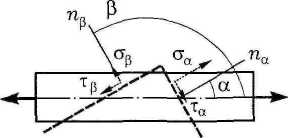
- •12 Напряжения на косых площадках. Теорема парности касательных напряжении nри растяжении-сжатии.
- •13 Потенциальная энергия деформации при растяжении-сжатии.
- •Диаграмма растяжения пластических материалов. Основные механические характеристики материалов
- •Диаграмма сжатия для пластических материалов. Разгрузка и повторное нагружение.Гипотеза упругой разгрузки. Эффект Баушингера (наклеп).
- •Диаграммы растяжения и сжатия хрупких материалов и основные механические характеристики. Особенности разрушения хрупких материалов.
- •Влияние фактора времени и температуры на механические характеристики материале. Понятие о ползучести, релаксации и длительной прочности.
- •20.Расчёт конструкций по методу предельных состояний. Допускаемые напряжения, их выбор.
- •21.Понятие о методе расчёта статически неопределимых систем по предельному состоянию, экономическая эффективность.
- •22.Деформация чистого сдвига .Закон Гука при сдвиге.
- •26. Задачи при расчете стержня на кручение:
- •27.Потенциальная энергия деформации
- •28 .Кручение стержня некруглого поперечного сечения
- •31. Главные оси инерции. Главные моменты инерции. Вычисление моментов инерции сложных сечений. Радиусы инерции.
- •32.Чистый изгиб прямого бруса в главной плоскости. Закон Гука при изгибе.
- •33.Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.
- •34. Нормальные напряжения при чистом изгибе. Жесткость при изгибе
- •35.Прямой поперечный изгиб. Распространение выводов чистого изгиба на поперечный изгиб.
- •36.Касательные напряжения при изгибе брусьев сплошных сечений(ф-ла Журавского). Распределение касательных напряжений по сечениям прямоугольного и двутаврового профиля.
- •37.Нормальные и касательные напряжения в сплошных и слоистых (листовой пакет) брусьях, прогибы в этих брусьях. Влияние касат.-х напряжений на эксплуатационные характеристики(гибкость, прогиб) рессоры.
- •38.Касательные напряжения в тонкостенных стержнях. Центр изгиба
- •39.Потенциальная энергия деформации при изгибе
- •40.Расчёты на прочность при изгибе.
- •41.Случаи, в которых необходима проверка прочности балок по касательным напряжениям.
- •42. Рациональные сечения при изгибе.
- •43.Понятие о кривом брусе большой и малой кривизны. З-н Гука для бруса большой кривизны. Связь изгибающего момента и нормальных напряжений для кривого бруса. Эпюра нормальных напряжений.
- •44.Определение нулевой линии для некоторых видов поперечных сечений бруса большой кривизны.
- •45. Дифференциальное уравнение упругой линии балки. Его непосредственное интегрирование. Граничные условия.
- •47. Теорема о взаимности работ(теорема Бетти)
- •47. Теорема о взаимности перемещений (теорема Максвелла)
- •Определение перемещений методом интеграла Мора.
- •Правило Верещагина.
- •51. Формула Cимпсона, Мюллера-Бреслау.
- •52. Основы метода сил.
- •53. Матрица податливости. Механический смысл коэффициентов матрицы податливости, приемы вычисления коэффициентов.
- •54. Основы метода перемещений. Канонические уравнения метода перемещений.
- •55. Матрица жесткости. Механический смысл коэффициентов матрицы жесткости, приемы вычисления коэффициентов.
- •56 Общий случай напряженного состояния в точке. Понятие о тензоре напряжений. Закон парности касательных напряжений.
- •57. Напряжения на произвольно ориентированной (косой) площадке.
- •59 Вековое уравнение. Инварианты тензора напряжений. Классификация видов ндс по инвариантам тензора напряжений.
- •6 0) Напряжения на октаэдрических площадках.
- •61.Площадки с наибольшими касательными напряжениями
- •62..Главное значение тензора напряжений.Положение главныхплощадок при плоском ндс
- •63 Площадки с наибольшими касательными напряжениями (площадки сдвига), их положение при плоском ндс.
- •64 Разложение тензора напряжений на шаровой тензор и девиатор напряжений. Интенсивность напряжений
- •65.Понятия о деформированном состоянии в точке
- •66 Перемещение, относительные деформации и сдвиги
- •69. Обобщенный закон Гука.
- •70. Объемная деформация. Закон Гука для объемной деформации.
- •71.Полная потенциальная энергия деформации. Потенциальная энергия изменения объема и формы.
- •72. Классификация напряженных состояний. Понятие об эквивалентном напряжении.
- •73.Сложное сопротивление: косой изгиб. Определение напряжений и положения нейтральной линии при косом изгибе.
- •74.Сложное сопротивление: внецентральное растяжение сжатие. Определение напряжений и положений нейтральной линии при внецентральном растяжении –сжатии. Ядро сечения.
Напряжения в поперечных сечениях бруса.
Продольная сила N является равнодействующей элементар-ных внутренних сил в сечении растянутого стержня, она связана с нормальными напряжениями зависимостью
![]()
![]()
Используя принцип Сен-Венана и условие однородности стержня, предполагаем, что внутренние силы распределены по поперечному сечению равномерно. Следовательно, нормальные напряжения σ при центральном растяжении-сжатии во всех точках сечения одинаковы. Это позволяет в выражении для N вынести σ за знак интеграла:
![]()
откуда σ=N/A , где А - площадь поперечного сечения.
Замечание. Если по длине стержня продольная сила N и площадь сечения А постоянны, то в стержне возникает однородное напряженное состояние, т. е. напряжения одинаковы во всех точках всех поперечных сечений.
Если же по длине стержня площадь поперечного сечения А переменна или вдоль оси приложены внешние нагрузки, то напряжения будут различными для разных поперечных сечений. Напряженное состояние в стержне будет неоднородным.
Продольные и поперечные деформации бруса. Закон Гука при растяжении и сжатии.
П![]() родольные
деформации.
Предположим,
что до нагружения длина стержня была
равна l.
Под воздействием
силы F
его длина
увеличилась
на Δl
и стала I
+ Δl
.
родольные
деформации.
Предположим,
что до нагружения длина стержня была
равна l.
Под воздействием
силы F
его длина
увеличилась
на Δl
и стала I
+ Δl
.
![]()
 Величину Δl
называют абсолютным
удлинением
стержня. Вследствие однородного
напряженного состояния все участки
растянутого стержня находятся в
одинаковых условиях, поэтому и
линейная деформация
Величину Δl
называют абсолютным
удлинением
стержня. Вследствие однородного
напряженного состояния все участки
растянутого стержня находятся в
одинаковых условиях, поэтому и
линейная деформация ![]() по оси стержня будет постоянной, равной
своему среднему значению:
ε
=
Δl / l
по оси стержня будет постоянной, равной
своему среднему значению:
ε
=
Δl / l
Эта величина называется относительным удлинением (относительной деформацией) стержня.
Если в стержне возникает неоднородное напряженное состояние, деформация в сечении определяется предельным переходом к малому участку длиной dz ε=Δ(dz)/dz , где Δ(dz) – удлинение элемента dz.
Поперечные
деформации.
Удлинение
стержня в направлении оси z
сопровождается уменьшением его
поперечных размеров
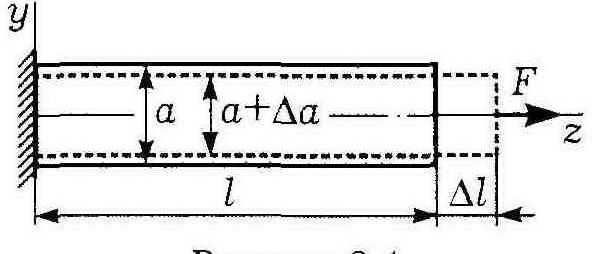 Таким
образом, при растяжении возникает
не только продольная εz=ε=Δl/l,
но и поперечная деформация стержня
εx=εy=Δa/a
Таким
образом, при растяжении возникает
не только продольная εz=ε=Δl/l,
но и поперечная деформация стержня
εx=εy=Δa/a
Экспериментально установлено, что в пределах применимости закона Гука поперечная деформация пропорциональна продольной:
εx=εy= -vε
где v - коэффициент Пуассона (безразмерная константа упругости материала).
Закон Гука при растяжении-сжатии
Напряжения и деформации линейно связаны между собой законом Гука, который подтвержден экспериментально и при растяжении-сжатии стержня имеет вид σ=Eε,
где Е - модуль Юнга (физическая константа материала, измеряется в Па. Например, для стали Е = 2.06*10^11
11 Удлинение (укорочение) бруса постоянного поперечного сечения. Жесткость при растяжении и сжатии. Перемещения поперечных сечений бруса.
Удлинение участка стержня. Подставим выражение для деформации ε=Δ(dz)/dz в закон Гука σ=Eε (1). Тогда, учитывая соотношение σ=N/A , получим полное удлинение участка стержня длиной l :
Δ(dz)=Ndz/EA;
![]() (2)
(2)
Из выражения (2) можно получить формулу для удлинения участка стержня при N = const, A= const:
Δ=Nl/EA (3)
где ЕА - жесткость поперечного сечения стержня при растяжении-сжатии.
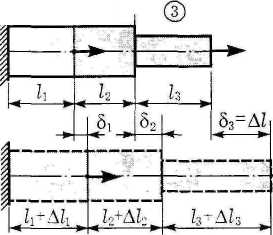
Перемещения сечений стержня. Часто требуется найти перемещения точек оси, а также полное удлинение стержня, состоящего из нескольких участков. Границами участков служат сечения, где приложены внешние силы или меняется жесткость сечения (рисунок 2.5).
В соответствии с (3) удлинение i-го участка стержня
Δli= Nili/ ЕAi
где Ni - продольная сила на i-м участке (Ni = const); li , ЕАi - длина и жесткость i-ro участка (ЕАi = const).
 ®
©
®
©
Перемещение δi, сечения стержня, находящегося на границе i-го участка, состоит из удлинения этого участка и перемещения его как единого целого за счет деформирования предыдущих участков:
δi= δi-1+Δli= δi-1+Ni ili/EAi
(i=1,…,n; δ0) (4)
По полученным результатам строят эпюру продольных перемещений (эпюру δ), т. е. график, изображающий изменение этих перемещений по длине оси бруса.
Полное удлинение стержня, состоящего из п участков, равно перемещению крайней точки последнего участка:
Δl=δn=∑Δli = ∑Ni l I /EAi
т. е. полное удлинение стержня, состоящего из нескольких участков, определяется алгебраическим суммированием удлинений участков.
