72. Классификация напряженных состояний. Понятие об эквивалентном напряжении.

Будем подразумевать под опасным состоянием материала, появления в нем зоны или области пластических деформаций, появление трещин, а так же саморазрушения материала. При этом происходит изменение механического состояния материала.

Можно однозначно утверждать что причиной изменения материала является напряженное состояние в точке. Проблема состоит в том что необходимо установить определенную меру напряженного материала которая будет предельной.

Следует заметить что главные напряжения и главные напряжении площадок могут характеризовать полное напряженное состояния в точках

1) это одноосное напряженное состояние

2) плоское напряженное состояние

3) объемное напряженное состояние

Если при одноосном напряженном состоянии не составит труда ответить на вопрос, когда возникнет опасное состояние разрушения материала.

То в случае 2),3) о наступлении опасного состояния в материале за чистую невозможно.

В этой связи возникла потребность в разработке так называемых теорий прочности, которые позволяют отценить возможное наступление опасного состояния.

Расширим понятие коэффициента запаса прочности, будем увеличивать компоненты какого-либо напряжённого состояния пропорционально друг другу. Наконец в какой то момент механическое состояние материала изменится, там возникнут пластические деформации, потом появятся трещины и наконец материал разрушится.

Условимся понимать под коэффициентом запаса в данном напряженном состоянии число показывающее во сколько раз увеличить напряженное состояние чтобы изменить его механическое состояние.

Обычно сравнивание напряженных состояний проводят не по коэффициенту запаса, а по эквивалентным напряжениям.

Эквивалентное напряжение- это напряжение которое необходимо создать в растянутом образце чтобы его состояние было равноопасно заданным напряженным состояниям.

Вводя понятие эквивалентного напряжения мы сводим расчет при сложном напряженном состоянии, к расчету на обычное растяжение. Выражение через главные напряжения

73.Сложное сопротивление: косой изгиб. Определение напряжений и положения нейтральной линии при косом изгибе.

Косым изгибом называется такой вид деформирования, при котором плоскость действия изгибающего момента М не совпадает ни с одной из главных плоскостейстержня. При косом изгибе есть единая для всего бруса силовая плоскость, т.е. во всех сечениях углы между линиями действия сил и главными центральными осями одинаковы.В случае пространственного косого изгиба нагрузки располагаются в разных продольных пл-тях,

из-за этого указанные углы не постоянны по длинне бруса.При поперечном косом изгибе, независимо от того, плоский он или пространственный, возникает четыре силовые 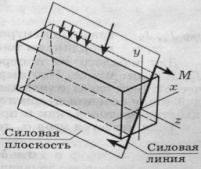фактора:изгибающие моменты и поперечные силы .Однако влияние поперечных сил незначительно и в расчетах на прочность и жесткость им, как правило, пренебрегают. Косой изгиб удобно рассматривать как одновременный изгиб в двух главных плоскостях zx и zy. Для этого изгибающий момент M в соответствии с принципом суперпозиции раскладывают на две составляющие

.где - моменты в вертикальной и горизонтальной плоскостях.

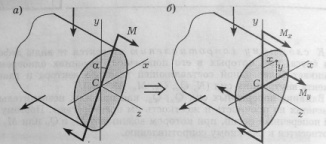
На основании принципа суперпозиции нормальные напряжения определяются как сумма напряжений от каждого из моментов

Для каждого из поперечных сечений бруса величины изгибающих моментов и моментов инерции постоянны. Поэтому уравнение полученное выше с точки зрения аналитической геометрии описывает плоскость. Следовательно, если в каждой точке сечения отложить по нормали к сечению вектор , то концы этих векторов, как и прямом изгибе, образуют плоскость. Если известен угол то получаем

Уравнение нулевой линии

Из уравнения следует, что нейтральная линия проходит через центр тяжести поперечного сечения и делит его на растянутую и сжатую части. При этом напряжения достигают экстремальных значений в точках сечения, наиболее удаленных от нулевой линии. Для сечения простой формы эти точки устанавливаются визуально, для сложных – с помощью прямых линий, проведенных параллельной нулевой. 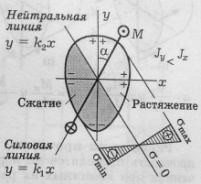Эпюра нормальных напряжений между этими линиями. В общем случае нулевая линия не перпендикулярна к плоскости изгибающего момента, как при прямом изгибе. Угловые коэффициенты