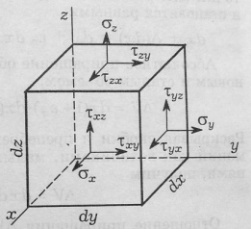
69. Обобщенный закон Гука.
Д
о
сих пор напряженное и деформированное
состояния рассматривались независимо
друг от друга и не связывались со
свойствами материала. Однако между ними
существует определенная зависимость.
В пределах малых деформаций эта
зависимость является линейной и носит
название обобщенного закона Гука. Для
вывода соответствующих соотношений
воспользуемся принципом суперпозиции
и рассмотрим раздельно воздействие
сил, возникающих на гранях элементарного
параллелепипеда, вырезанного в изотропном
теле вокруг рассматриваемой точки. За
счет нормальных напряжений происходят
растяжение и сжатие вдоль координатных
осей, но не искажаются первоначально
прямые углы между этими осями. Касательные
напряжения обусловливают искажение
соответствующих углов, но не влияю на
изменение внешних размеров. При этом
касательное напряжение , действующее
в одной координатной плоскости, не
связано со сдвигом с другой координатной
плоскости. Просумируем линейные
деформации вдоль оси х, вызванные всеми
нормальными напряжениями. За счет
напряжения
параллелепипед
растягивается на определенную величину
/Е.
Напряжения
растягивают
его вдоль осей y
и z
соответственно, следовательно вдоль
оси x
за счет этого происходит сжатие.Соответствующие
деформации отрицательны и равны
.Поэтому
суммарная деформация вдоль оси х .
А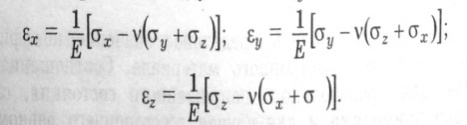
налогично
выражения следуют и для
Касательные напряжения и сдвиги можно связать соотношениями
Полученные соотношения являются аналитическим выражением обобщенного закона Гука для изотропного тела.
70. Объемная деформация. Закон Гука для объемной деформации.
Наряду с линейной и угловой деформациями в сопротивлении материалов приходится иногда рассматривать объемную деформацию , т.е. относительное изменение обьема в точке. Линейные размеры элементарного параллелепипеда dx,dy,dz,:
Абсолютное приращение объема вычисляется как разность между новым и старым объемом:
Раскрывая скобки и пренебрегая произведениями линейных деформаций как величинами, малыми по сравнению с их первыми степенями
Отношению
приращения
к
первоначальному объему паралелипипеда
V
называется объемной деформацией
.Она
равна сумме трех линейных осевых
деформаций
При повороте осей координат величина объемной деформации в точке не изменяется, так как совпадает по величине с первым инвариантом тензора деформаций.
Выражение объемной деформации через нармальные напряжения получим, соотношение обобщенного закона Гука.
Отсюда
можно установить предельное значение
коефициента для любого изотропного
материала.Соотношение применимо для
произвольного состояния, следовательно,
оно применимо и для случая всестороннего
равномерного растяжения
Так как величина p>0 то и объемная деформация также должна быть положительной.Это возможно, если 1-2v>0.Следовательно ,значение коэффициента Пуассона не может привышать 0.5.
71.Полная потенциальная энергия деформации. Потенциальная энергия изменения объема и формы.
В общем случае объемного напряженного состояния потенциальная энергия деформации, накопленная в элементарном объеме, определяется суммой работ всех сил, действующих по граням паралелипипеда.
Определим
работу, относящуюся к напряжению
.Соответствующая ему элементарная
средняя сила 0.5
dydz
совершает работу на перемещение
.
Эта работа имеет величину
0.5
dydz
Аналогичные
выражения работ дают и остальные
нормалные составляющие. Средняя
касательная сила
Выражение остальных работ получаем простой перестановкой индексов.В результате имеем.
Если энергию отнести к объему параллелепипеда dxdydz и с помощью закона Гука выразить деформации через напряжения, получим удельную потенциальную энергию единицы объема
Через главные напряжения удельная потенциальная энергия выражается в виде
Полную
потенциальную энергию получим,
проинтегрировав удельную деформацию
по объему деформированного тела.Деление
потенциальной энергии
на
энергию изменения объема
и
энергию формоизменения
т.е.
является условным и потребуется в дальнейшем при изучении предельных напряженных состояний .
Потенциальную энергию изменения объема получим как работу среднего напряжения
на объемной деформации
В главных осях вид формулы не изменяется, только координатные напряжения заменятся на главные.Энергию формоизменении находим как
В частном случае встречного равномерного растяженили сжатия получим
При чистом сдвиге присутствуют только касательные напряжения. Поэтому составляющие потенциальной энергии имеют вид
