64 Разложение тензора напряжений на шаровой тензор и девиатор напряжений. Интенсивность напряжений

Разложение тензора напряжений на шаровую и девиаторную части имеет большое принципиальное значение при иссле­довании поведения упругих и пластических тел под нагрузкой.

Шаровая часть выделяет из напряженного состояния равномер­ное всестороннее растяжение или сжатие, при котором изменя­ется лишь объем данного элемента тела без изменения формы.

Д евиатор напряжений характеризует состояние сдвига, при ко­тором изменяется форма элемента без изменения его объема.

Следовательно, девиатор напряжений указывает отклонение (девиацию) рассматриваемого напряженного состояния от все­стороннего растяжения (сжатия) или отклонение приобретен­ной формы тела от первоначальной. Как показывают опыты, материалы по-разному реагируют на всестороннее сжатие и на

напряжение сдвига.

По аналогии с инвариантами тензора напряжений построим инварианты для введенных тензоров. Первый инвариант шаро­вого тензора совпадает с первым инвариантом тензора напря­жений: J=σ11+σ22+σ33

Интенсивность напряжений-величина, определяющая касат. напряжение на элем. площадке, одинаково наклонённой к гл. осям напряжений в точке (октаэдрич. касат. напряжение). Через компоненты тензора напряжений sij И. н. sij выражается ф-лой: Применяется в пластичности теории.

65.Понятия о деформированном состоянии в точке

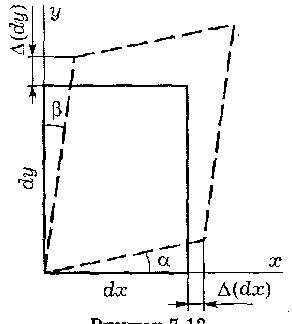
Тензор деформаций. Проведем через рассматриваемую точку тела сечение и возьмем в его плоскости прямоугольник с взаимно перпендикулярными элементами dx, dy (рису- нок 7.12). Через Δ(dх), Δ(dy) обозначим изменения длин волокон, а через а, β - углы их поворота после приложения нагрузки. Тогда угловой γ_xy и линейными ε_x, ε_y деформациями будут следующие величины:

В общем случае пространственного элемента (параллелепипеда) линейная ε_z и сдвиговые γ_yz, γ_zx « деформации вводятся по аналогии. Совокупность всех деформаций полностью описывает деформированное состояние в точке тела, т. е. по этим шести компонентам можно найти удлинение любой оси и углы сдвига в любых плоскостях, проходящих через рассматриваемую точку.

66 Перемещение, относительные деформации и сдвиги

Пусть точка находится в не деформированном теле. После нагружения тело деформируется, и точка меняет своё место положение. Расстояние от точки до деформации, до точки после деформации и называется перемещением.

Сдвиг-это изменение угла в той или иной координатной плоскости

Относительная деформация- отношение величины изменения размера тела к его исходному размеру.

6 7. Тензор деформаций. Главные значения и инварианты тензора деформаций.

. Главные значения тензора напряжений и инварианты тензора деформаций.

Проведем через рассматриваемую точку тела сечение и возьмем в его плоскости прямоугольник с взаимно перпендикулярными элементами . Через обозначим изменения длин волокон, а через углы их поворота после приложения нагрузки. Тогда угловой и линейными деформациями будут следующие величины:

В общем случае пространственного элемента линейная и сдвиговые деформации вводятся по аналогии. Совокупность всех деформаций , , , образуют тензор деформаций , матрица которого записывается в виде

Тензор деформаций обладает свойствами, свойствами совершенно аналогичными свойствам тензора напряжений. У него также в каждой исследуемой точке тела существуют три взаимно перпендикулярные оси, в которых угловые деформации отсутствуют. Эти оси называются главными осями тензора деформаций.

Матрица тензора деформаций в главных осях принимает следующий вид

И х величины вычисляются как корни кубического уравнения, аналогично вековому уравнению тензора напряжений

В главных осях они принимают вид:

В упругой области главные оси и главные площадки тензоров напряжений и деформаций совпадают. При малых упругопластических деформациях соостность тензоров наблюдается в области простых нагружений когда все компоненты тензора напряжений изменяются пропорционально одному общему параметру, например, время.Следует отметить, что для конструкционных материалов величина линейной деформации в упругой области весьма мала и составляет доли процента.

68. Шаровой тензор и девиатор деформаций. Интенсивность деформаций.

Интенсивность деформаций.

Шаровой тензор деформаций

Девиатор тензора деформаций

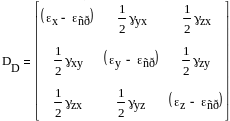
Девиатор тензора деформаций характеризует изменение формы при постоянном объеме

Интенсивность деформаций

В теории пластичности, а так же в некоторой теории прочности используют понятие интенсивность

Например при чистом сдвиге в координатной плоскости xy интенсивность сдвиговой деформации

Кроме интенсивности сдвиговой деформации, вводят понятие интенсивности линейной деформации

В главных осях эти выражения упрощаются