59 Вековое уравнение. Инварианты тензора напряжений. Классификация видов ндс по инвариантам тензора напряжений.

(7.8)

6 0) Напряжения на октаэдрических площадках.

При изучении сложного деформирования брусьев с учетом пла- стических деформаций оказывается важным знать напряжения на площадках, равнонаклоненных к главным осям тензора напряжений. Такие площадки называются октаэдрическими, так как они параллельны грани октаэдра, образованного из куба.

Нормаль к октаэдрической площадке образует равные углы с главными осями, следовательно, ее направляющие косинусы одина- ковы: l ^2= т^2 = n ^2= 1/3. Подставив эти значения в формулы

получим нормальные и касательные напряжений на октаэд- рической площадке:

напряжение a_oct представляет собой среднее нормальное напряжение для данного объемного напряженного состояния.

Октаэдрические напряжения являются инвариантными величи- нами и выражаются через инварианты тензора напряжений

61.Площадки с наибольшими касательными напряжениями

Особый интерес представляют площадки, на которых возникают максимальные касательные напряжения. Положение этих площадок можно определить, исследуя выражение

Заметим, что

Так как квадрат числа не меньше суммы квадратов чисел, его составляющих, то

Чтобы ТАО, достигла максимума, необходимо увеличить большее из слагаемых. Это достигается ростом произведения I^2*n^2 за

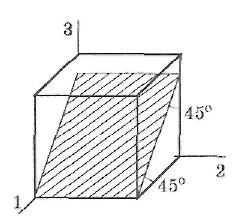счет т^2 . Максимум будет при Тогда Следовательно, площадка с максималь- ным касательным напряжением равнонаклонена к площадкам, на которых действуют максимальным касательным напряжениям равно наклонена к площадкам на кот. действуют максимальное и минимальное из главных напряжений, и параллельна оси 2

62..Главное значение тензора напряжений.Положение главныхплощадок при плоском ндс

Плоское напряжённое состояние-это состояние,когда в точке все напряженияна одной из координатных плоскостей=0.

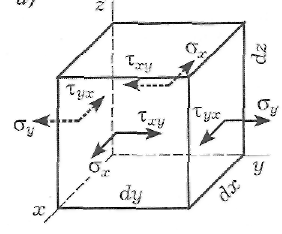
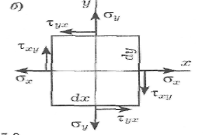
З десь ось z является главной, так как на соответствующей площадке все касательные напряжения равны ну- лю. Инварианты тензора напряжений принимают значения

уравнение сводится к квадратному

Корни этого уравнения

63 Площадки с наибольшими касательными напряжениями (площадки сдвига), их по­ложение при плоском ндс.

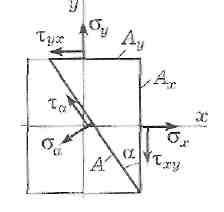
Определим касательные напряжения на косой площадке, наклоненной к оси у под углом α. Рассмотрим равновесие треугольного элемента, отсеченного этой косой площадкой. Потребуем равенства нулю суммы проекций всех действующих сил на направление :

где А, Ах, Ау - площади соответствующих площадок , причем . Отсюда, сокращая на А, получим

Или

Н а главной площадке касательные на- пряжения обращаются в нуль. Предположив, что рассматриваемая косая площадка являет- ся главной, и положив в последней формуле тао_а = 0, получим Следовательно, если площадку с напряжением с_х повернуть на угол а, определенный из соотношения (7.18), то получим главную площадку. При а > 0 поворот осуществляется против часовой стрелки, при а < 0 - по часовой стрелке. Вторая главная площадка будет перпендикулярна найденной.