56 Общий случай напряженного состояния в точке. Понятие о тензоре напряжений. За­кон парности касательных напряжений.

Совокупность всех напряжений, возника­ющих на множестве площадок, проходящих через рассматриваемую точку, называется напряженным состоянием в точке. Для его описания вырежем вокруг точки элементарный параллелепи­пед, ребра которого параллельны координатным осям и имеют малые ддины dx, dy, dz (рисунок 7.1, а). В силу малости параллелепипеда можно считать, что напряжения на его гранях совпадают с напряже­ниями на параллельных им коор­динатных площадках, проведенных через рассматриваемую точку.

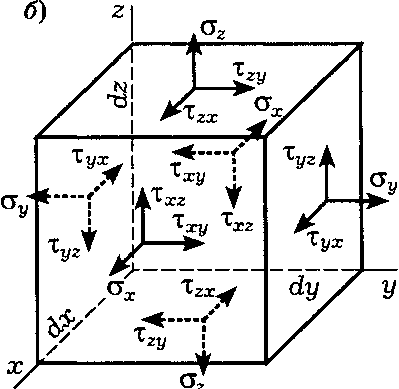
Действующие на гранях парал­лелепипеда напряжения можно раз­ложить на нормальные δ (перпенди­кулярные к граням) и касательные τ (лежащие в плоскости граней) со­ставляющие (рисунок б).

Нормальное напряжение имеет один индекс, указывающий ось, ко­торой оно параллельно. Для обозна­чения касательного напряжения применяют два индекса: первый указывает на нормаль к площадке, на которой действует напряжение; второй индекс обозначает ось, кото­рой оно параллельно.

Одноименные напряжения, которые действуют на противополож­ных гранях малого параллелепипеда, мало отличаются друг от друга, поэтому считаем их одинаковыми. Совокупность напряжений на гранях параллелепипеда образует тензор напряжений Т_δ:

В строках содержатся компоненты тензора напряжений, действую­щие на одной площадке, в столбцах - параллельные одной коорди­натной оси.

Теорема парности касательных напряжений. Рассмотрим ус­ловия равновесия выделенного параллелепипеда. Уравнения для сил выполняются тождественно, так как для каждой компоненты на­пряжений существует такая же по величине компонента, противопо­ложно направленная и действующая на грани такой же площади (силами являются произведения напряжений на площади соответст­вующих граней). Из уравнения равновесия моментов сил относи­тельно оси х следует

τ_yz dx dz dy - τ_zy dx dy dz = 0,

отсюда τ_yz = τ_zy.

Составляя аналогичные уравнения относительно осей у и z, по­лучим, что τ_xy=τ_yx, τ_zx =τ_xz. Этот результат носит название тео­ремы парности касательных напряжений: одно­именные касательные напряжения, действующие на двух взаимно перпендикулярных площадках, равны по величине и одновременно направлены либо к общему ребру, либо от него.

Теорема парности касательных напряжений справедлива для всех точек нагруженного тела, независимо от вида приложенных нагрузок и свойств материала.

С ледствие. Матрица тензора напряжений симметрична относительно своей главной диагонали. Независимыми в ней явля­ются шесть компонент: δ_х, δ_у, δ_z, τ_xy, τ_yz, τ_zx.

Вектор можно задать тремя компонентами - числами, то тензор задается тремя векторами или девятью числами.

Перемещением данной точки сооружения называется из­менение ее координат, вызванное деформацией системы. Переме­щения могут быть линейными и угловыми.

57. Напряжения на произвольно ориентированной (косой) площадке.

Через любую точку твердого тела можно провести бесконечное множество площадок. Выделим одну из них и рассмотрим элемен­тарную пирамидку, образованную координатными гранями и произ­вольной площадкой (рисунок 7.2, а).

Пусть нормаль v к площадке со­ставляет с осями координат углы, коси­нусы которых обозначим l, т, п:

cos(v, х) = l; cos(v, у) = т ; cos(v, z)=n.

Величины l, m, n называются направ­ляющими косинусами нормали v. Для них выполняется известное из гео­метрии условие l² + m² + n² = 1.

Площадь косой площадки обозначим А. Площади координатных граней А_х, А_у, A_z (индекс указывает нормаль к площадке) связаны с А следующими со­отношениями:

А_х = Аl; А_у= Am; A_z = An . (7.3)

Приложим к выделенной элементар­ной пирамиде действующие на ее гранях напряжения (рисунок 7.2, б). Проекции вектора полного напряжения p_v на ко­сой площадке обозначим p_vx, p_vz, p_vz.

Рассмотрим условия равновесия пирамиды. Составим суммы про­екций сил на координатные оси х, у, z:

p_vxA – σ_xA_x – τ_yxA_y – τ_zxA_z = 0

p_vzA – τ_xyA_x – σ_yA_y – τ_zyA_z = 0 (7.4)

p_vz A – τ_xzA_x– τ_yzA_y – σ_zA_z = 0

Подставим в систему (7.4) соотношения (7.3). Сократив их на А, получим выражения для компонентов вектора напряжения на про­извольной косой площадке через координатные напряжения:

p_vx = σ_xl + τ_yxm + τ_zxn

p_vz = τ_xyl + σ_ym + τ_zyn (7.5)

p_vz = τ_xzl + τ_yzm + σ_zn

Модуль полного напряжения на площадке

Т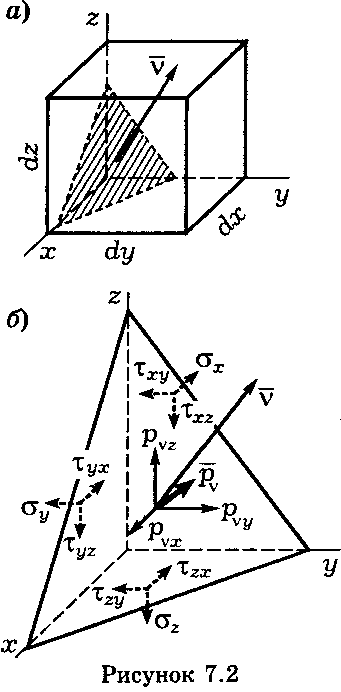 аким образом, с помощью компонентов тензора напряжений на трех координатных площадках можно полностью описать напряжен­ное состояние в точке, т. е. определить напряжения на любой пло­щадке, проведенной через рассматриваемую точку.

58.   Эллипсоид напряжений.    

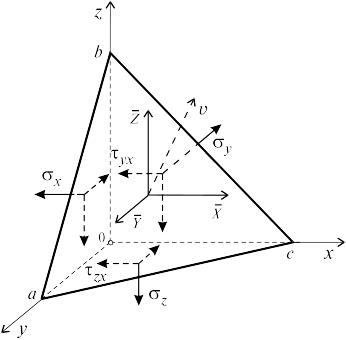
Из напряженного тела в окрестности произвольной точки вы­делим элементарныйобъем в виде тетраэдра (рис. 10.2).

      Ориентация площадки в пространстве задается направляющими косинусами нормали v к ней  l = cos (x, v), m = cos (y, v), n == cos  (z, v).

      Вектор полного напряжения на произвольной площадке abc спроецируем на оси x, y и z. Обозначим эти проекции через , , . Обозначая площадь треугольников abc, a0b, b0c, a0c через dF, dFx , dFy , dFz , соответственно будем иметь:

dFx = dFl;     dFy = dFm;     dFz = dFn.                     (10.3)

      Проецируя все силы, действующие на выделенный элемент, по­следовательно на оси x, y, z и с учетом (10.3) получим: X = _x  l + _yx  m + _zx  n; Y = _yx  l + _y  m + _zy*n;                    (10.4) Z = _zx  l + _zy  m + _z n.

      Выразим нормальное напряжение v на наклонной площадке через X, Y, Z:

_v = X  l + Y  m + Z  n (10.5)

      Отcюда, с учетом (10.3) получим

_v = _x l ² + _y m ² + _z n ² + 2 _yzmn + 2 _zxnl + 2 _xylm .              (10.6)

       Рассмотрим множество секущих площадок произвольнойори­ентации, проходящих через исследуемую точку. По нормали к каж­дой площадке отложим отрезок r = f (_v ), координаты конца век­тора которого будут следующими: x = r  l;    y = r  m;    z = r  n.

      Исключая из (10.6) направляющие косину­сы, получим

      _v r ² = _x x ² + _y y ² + _z z ² + 2 _yzy z + 2 _xyx y + 2 _xzx z .     (10.7)

Принимая

обозначение

,

где k  произвольная постоянная, из (10.6) получим:

_x x ² + _y y ² + _z z ² + 2 _yzy z + 2 _xyx y + 2 _xzx z = k.                       (10.8)

      Из курса аналитической геометрии известно, что (10.8) пред­ставляет собой уравнение поверхности второго порядка в системе координат x, y, z. Следовательно путем поворота системы коорди­нат уравнение (10.8) можно преобразовать таким образом, чтобы попарные произведения исчезли, или иначе говоря коэффициенты попарных произведений принимали нулевые значения.

      Это значит, что в произвольной точке напряженного тела суще­ствует такое положение системы координат x, y, z, в которой каса­тельные напряжения _xy , _xz , _yz  равны нулю. Такие оси называются главными осями. Соответствующие им взаимно перпендикулярные площадки называются главными площадками, а нормальные напряжения на них  главными напряжениями. Принимаются такие обозначения: 1  2  3.

      Если в окрестнос­ти рассматриваемой точки определены по­ложение главных пло­щадок и главные на­пряжения, то сущест­венно упрощается си­стема уравнений (10.4). Они принимают вид: X = ₁  l;   Y = ₂  m; Z = ₃   n.

.

      Так как l 2 + m 2 + + n 2 =1, то получим:

.

С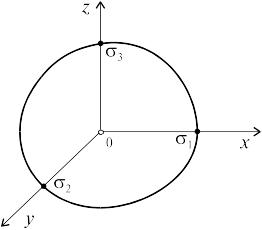 ледовательно, гео­метрическое место концов вектора пол­ного напряжения Р (X, Y, Z) об­разует эллипсоид, полуосям ко­торого являются главные напря­жения ₁, ₂, ₃ (рис. 10.3). Полученный эллипсоид носит название эллипсоида напря­жений. В случае равенства двух главных напряжений эллипсоид принимает форму тела враще­ния. Тогда каждая плоскость, проходящая через ось вращения становится главной. В случае, если все три главных на­пряжения равны между собой, то эллипсоид принимает форму сферы и в исследуемой точке все плоскости являются главным