41.Случаи, в которых необходима проверка прочности балок по касательным напряжениям.

Для тонкостенных профилей (швеллер, двутавр, уголок и др.) необходимо дополнительно выполнять проверку прочности по касательным напряжениям. Условие прочности по τ имеет вид:

Где τmax—максимальное касательное напряжение в опасном сечении;

Qymax—наибольшая по абсолютному значению поперечная сила;

[τ]—допускаемые касательные напряжения;

Jx—момент инерции этого сечения относительно главной центральной оси;

δ—толщина сечения на уровне, где определяется τ;

Sx—статический момент отсеченной части поперечного сечения.

42. Рациональные сечения при изгибе.

Чтобы форма сечения по возможности была рациональной, необходимо распределять

площадь сечения подальше от нейтральной оси. Так возникли стандартные тонкостенные профили, такие, как двутавры и швеллеры. При изгибе балок в вертикальной плоскости такие профили дают существенную выгоду по сравнению с прочими формами поперечных сечений.

43.Понятие о кривом брусе большой и малой кривизны. З-н Гука для бруса большой кривизны. Связь изгибающего момента и нормальных напряжений для кривого бруса. Эпюра нормальных напряжений.

Кривизной стержня наз. величина, обратная радиусу кривизны его центральной оси 1/ρ0.

Различают следующие типы кривых стержней:

Стержни большой кривизны (0,2<h/ρ0≤1);

Стержни малой кривизны(0,1<h/ρ0≤0,2).

h—наибольшая высота сечения.

З-н Гука для бруса большой кривизны:

Изгибающий момент явл. Интегральной характеристикой действующих в поперечном сечении нормальных напряжений и следует из соотношения

44.Определение нулевой линии для некоторых видов поперечных сечений бруса большой кривизны.

Уравнение нулевой (нейтральной) линии :

Из уравнения следует, что нулевая линия не проходит через центр тяжести сечения. Она делит сечение на растянутую и сжатую части. Если продольная сила N<0 (изгиб со сжатием), то площадь сжатой зоны будет больше, чем площадь растянутой. При N>0 (изгиб с растяжением)—наоборот.

45. Дифференциальное уравнение упругой линии балки. Его непосредственное интегрирование. Граничные условия.

Из курса математического ана­лиза известно, что кривизна l/р некоторой линии у = y{z) связана с уравнением кривой соотношением

С другой стороны

Приравнивая правые части этих формул, получаем точное дифференциальное уравнение упругой линии балки:

Уравнение нелинейное, его интегрирование связано с боль­шими трудностями. Однако из-за малости углов поворота θ(z) = у' их квадратами можно пренебречь как величинами весьма малыми по сравнению с единицей. Тогда это уравнение упрощается:

Выбор знака зависит от принятой системы координат. Если внутренний изгибающий момент направлен так, что увеличивает кривизну изогну­того стержня, то в последнем уравнении следует сохранить только знак «плюс»:

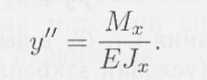
Это уравнение называется дифференциальным уравне­нием упругой линии балки. Оно является приближенным, так как использовано допущение о малости углов поворота. Кроме это­го, не учтены деформации сдвига, связанные с наличием поперечных сил. Однако в подавляющем большинстве случаев влияние поперечных сил несущественно и им можно пренебречь.

Перемещения балки при изгибе—прогиб y(z) и угол поворота сечения θ(z)—для нагрузок простого вида можно получить методом непосредственного интегрирования уравнения (1). Тогда в результате двукратного интегрирования имеем

Константы интегрирования С1,С2 определяются из граничных условий (условий закрепления стержня