37.Нормальные и касательные напряжения в сплошных и слоистых (листовой пакет) брусьях, прогибы в этих брусьях. Влияние касат.-х напряжений на эксплуатационные характеристики(гибкость, прогиб) рессоры.

В сплошных брусьях величины нормальных напряжений значительно больше, чем касательных. По этой причине расчеты на прочность при изгибе ведут по нормальным напряжениям(касательные напряжения на прочность не учитывают):

σ_мах=М_{х мах}/W_x≤{ σ }

Подобно деформации растяжения-сжатия кручению при изгибе в расчетах на прочность рассматривают следующие типы задач:

1)поверочные расчеты: определив в элементе конструкции σ_мах, сравнив его с величиной допускаемого напряжения , дают заключение:

σ_мах>{ σ }-прочность бруса не обеспечена

σ_мах<{ σ }- прочность обеспечена

2)проектировочный расчет: из условия прочности нужно подобрать размеры поперечного сечения балки, т.е. W_x≥ М_{х мах}/{ σ }

3)расчет на грузоподъемность: в этих задачах определяют величину допускаемого изгибающего момента:

{ М } = W_x *{ σ }.Ординаты эпюр могут быть выражены через Q или через М, или распределенные силы.

38.Касательные напряжения в тонкостенных стержнях. Центр изгиба

При распределении касательных напряжений в поперечных сечениях балки при поперечном изгибе напряжения τ параллельны поперечной силе Q_y.Если сечение представляет собой незамк­нутый тонкостенный профиль, то картина распределения касательных напряжений су­щественно меняется. В точках сечения вблизи наружного и внутреннего контуров напряжения т направ­лены касательно к контурам. Из-за малости толщины сечения δ можно считать, что τ постоянны по толщи­не и направлены по касательной к средней линии сечения.

Формула Журавского для тонкостенных стержней. Рассмот­рим элемент балки тонкостенного сечения, выделенный двумя сече­ниями z и z+ dz (рисунок а).

Вывод формулы Журавского производится по тому же принципу, что и для бруса сплошного сечения. Отличие здесь в выполнении продольного разреза, который следует проводить плоскостью, нор­мальной к срединной линии контура (рисунок б).

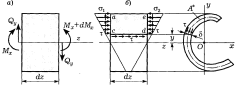
Приходим к формуле Журавского для тонкостенных стержней:

где Qy -абсолютная величина поперечной силы в том сечении, где вычисляются касательные напряжения;

I_x -момент инерции этого сечения относительно главной цен­тральной оси;

δ - толщина сечения на уровне, где определяются т;

S*_x -статический момент отсеченной части поперечного сечения.

39.Потенциальная энергия деформации при изгибе

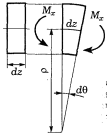
Энергия упругих деформаций элемента стержня dz при чистом изгибе определяется работой момента M_x на взаимном угловом пере­мещении dθ двух сечений

Отсюда следует выражение для элементарной потенциальной энергии

dU =M_х²dz /2EJ_х

Полную потенциальную энергию деформации получим, проин­тегрировав последнее выражение по длине балки l:

Если изгибающий момент и жесткость балки постоянны по ее длине, то следовательно:

Это же выражение определяет потенциальну

40.Расчёты на прочность при изгибе.

При изгибе в поперечных сечениях балки возникают нормальные и касательные напряжения. Рассматривая распределение σ и τ по сечению, можно заметить важную особенность:

Нормальные напряжения достигают своих наибольших значений в точках, наиболее удаленных от нейтральной оси; в этих точках касательные напряжения , как правило, равны 0 или малы;

Касательные напряжения обычно максимальны на нейтральной оси или вблизи нее, т.е. там, где нормальные напряжения равны 0 или малы.

Поэтому при расчете на прочность балок можно пренебречь взаимным влиянием нормальных и касательных напряжений и сформулировать раздельно условия прочности по нормальным и касательным напряжениям.