36.Касательные напряжения при изгибе брусьев сплошных сечений(ф-ла Журавского). Распределение касательных напряжений по сечениям прямоугольного и двутаврового профиля.

Касательные напряжения. Принимая гипотезу плоских сече­ний, считаем, что при деформации каждое продольное во­локно остается нормальным к поперечным сечениям. А это значит, что в плоскости zу деформации сдвига γ считаются равными нулю. Поперечная сила является равнодействующей элементарных рас­пределенных сил, лежащих в плоскости сечения:

Задача по определению напряжений всегда статически неопределима. Однако можно принять такие гипотезы о распределении напряже­ний, что задача станет статически определимой.

Двумя близкими поперечными сечениями выделим элемент бал­ки малой длины dz(рис.а) :

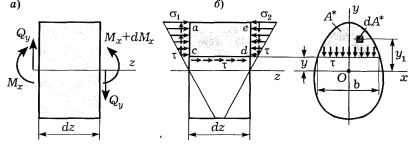
В левом и правом сечениях внутренние изгибающие моменты от­личаются на малую величину dM , а поперечные силы считаются постоянными. Проведем продольное сечение, образовав элемент acde. На грани ас возникают нормальные напряжения σ ₁ = (M_x / J_x)y\, на грани ed - σ ₂= [(M_x +dM_x)/J_x]U₁ (рисунок б).

Равнодействующая внутренних продольных сил, распределенных по левой грани (рис.):

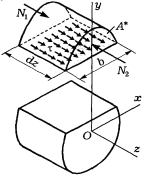
где А* - площадь отсеченной части

S_х* - статический момент отсечен­ной части сечения относи­тельно нейтральной оси

Аналогично на правой грани

Предположим, что касательные напряжения τ распределены по ширине поперечного сечения равномерно. Это допущение тем спра­ведливее, чем меньше ширина сечения по сравнению с его высотой h. Тогда равнодействующая касательных сил равна значению напря­жений, умноженному на площадь нижней грани: τ bdz.Составляем уравнение равновесия элемента:

Используя дифференциальную зависимость между поперечной силой и изгибающим моментом, получаем окончательное вы­ражение касательных напряжений в продольных сечениях балки:

Формула эта была предложена Д. И. Журавским , поэтому на­звана его именем.

Для произвольного поперечного сечения величины, входящие в формулу, имеют следующий смысл:

Qy - абсолютная величина поперечной силы в том сечении, где вычисляются касательные напряжения;

J_x - момент инерции этого сечения относительно его нейтраль­ной линии (главной центральной оси);

b - ширина сечения на уровне, где определяются τ;

S_х* - абсолютная величина статического момента отсеченной части поперечного сечения относительно нейтральной оси (той части площади А*, которая заключена между линией, где определяются τ, и краем сечения).

Распределение напряжений

по прямоугольному и двутавровому сечениям

При поперечном изгибе в сечениях балки присутствуют изги­бающий момент M и поперечная сила Q , следовательно, появляют­ся нормальные и касательные напряжения.

Прямоугольное сечение. Пусть сечение балки представляет со­бой прямоугольник со сторонами b и h (рисунок).

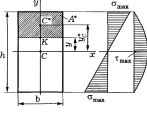
Нормальные напряжения распределены по высоте сече­ния линейно, достигая максимума на крайних волокнах,

где M - изгибающий момент в рассматриваемом сечении;

у - ордината точки в поперечном сечении;

J - момент инерции прямоугольника относительно главной центральной оси х; J_x = bh³/12 ;

W - момент сопротивления прямоугольника; W_x = bh²/6.

Касательные напряжения определяются формулой Журавского. Статический момент отсеченной части сечения вы­числяется как произведение заштрихованной площади на координа­ту ее центра тяжести:

Отсюда:

Следовательно, эпюра каса­тельных напряжений по высоте сечения ограничена параболой. Наибольшие напряжения имеют место при у= 0:

Двутавровое сечение. Пусть балка имеет двутавровое сечение. Приближенно принимаем его составленным из трех прямоугольников. Нормальные напряжения в нем, как и для прямоуголь­ного сечения, определяются соотношениями

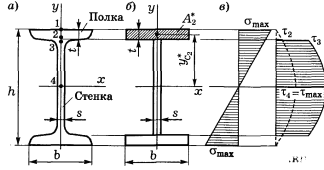
Эпюра σ прямолинейна, проходит через центр тяжести сечения.

Касательные напряжения вычислим по формуле Жyравского в указанных на рисунке четырех точках.

В верхней точке 1

,

для точки 2:

Аналогично, для точек 3 и 4 определяем касат. Напряжения

В точке 4, по сравнению с точкой 3, увеличится статический момент. Для стандартных двутавров его можно не вычислять, а взять из таблиц сортамента. По своей величине τ ₄ > τ _3. Эпюра касательных напряжений в пределах стенки двутавра ог­раничена параболой.