33.Дифференциальные зависимости между изгибающим моментом, поперечной силой и интенсивностью распределенной нагрузки.

Дифференциальные соотношения при прямом изгибе. Рас­смотрим балку, на которую действует плоская система сил, среди которой находится гладкая распределенная нагрузка q(z), направ­ленная вдоль оси у. Двумя близкими сечениями z и z + dz выделим малый элемент балки, к которому не приложены сосредоточенные силы и моменты.

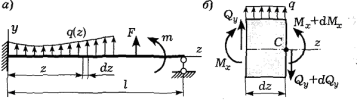
Вся балка находится в равновесии, поэтому в равновесии должен находиться и ее элемент dz. Приравниваем к нулю сумму проекций всех сил на ось у:

Отсюда:

т. е. первая производная от поперечной силы вдоль оси балки совпа­дает с величиной интенсивности распределенной нагрузки, перпенди­кулярной оси балки.Приравниваем к нулю сумму всех моментов относительно центра тяжести правого сечения (т.С):

т. е. первая производная от изгибающего момента вдоль оси балки представляет собой величину поперечной силы.

Из двух дифференциальных зависимостей легко вывести третью:

34. Нормальные напряжения при чистом изгибе. Жесткость при изгибе

Рассмотрим чистый изгиб в вертикальной плоскости, при кото­ром в сечениях балки возникает только изгибающий момент M_x. В сечениях присутствуют только нормальные напряжения σ.

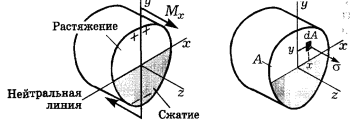
Выберем систему координат в по­перечном сечении балки, учитывая, что только M_x ≠0. Все осталь­ные внутренние силовые факторы, в том числе продольная сила N и изгибающий момент М_у, обращаются в нуль.

Продольную силу получим, проинтегрировав элементарную силу σdA по всей площади поперечного сечения А:

С учетом того, что

где:

- статический момент площади сечения.

Чтобы в сечении продольная сила не возникала (N = 0), статиче­ский момент должен быть равен нулю (S_x = 0), следовательно, вы­бранная система координат должна быть центральной.

Горизонтальный изгибающий момент получим, проинтегриро­вав момент элементарной силы xσdA:

Из закона Гука получим:

Где

- центробежный момент инерции.

Так как изгибающий момент в горизонтальной плоскости сече­ния My = 0, то следует, что центробежный момент инерции равен нулю (Jху = 0).Поэтому выбранная система координат должна быть главной.

Следовательно, прямой чистый изгиб бруса под действием изги­бающего момента M_x происходит только тогда, когда оси координат х, у являются главными центральными осями сечения.

Жесткость при изгибе:

1/ρ=±М_х/ЕI_x, где ЕI_x-жесткость сечения при изгибе, ρ-радиус кривизны изогнутой нейтральной оси балки, 1/ρ – кривизна балки при чистом изгибе.

35.Прямой поперечный изгиб. Распространение выводов чистого изгиба на поперечный изгиб.

Основное отличие поперечного изгиба от чистого состоит в том, что в первом случае в поперечных сечениях балки действует не только поперечный момент, но и сила Q- равнодействующая элементарных касательных сил, действующих в плоскости поперечного сечения.

Т.о., для данного вида деформации необходимо учитывать, кроме нормальных напряжений в поперечных сечениях действуют и касательные напряжения, наличие которых сопровождается появлением угловых деформаций. Кроме перемещений, свойственных чистому изгибу, появляется дополнительные угловые перемещения, обусловленные деформацией сдвига. Касательные напряжения распределены по высоте неравномерно, поэтому неравномерно распределены и угловые перемещения, это значит, что поперечные сечения при поперечном изгибе, в отличие от чистого изгиба, перестают быть плоскими, т.е. нарушается гипотеза плоских сечений Бернулли.

Однако, искривление плоских сечений заметно не скажется на величине нормальных напряжений. В частности, если на каком-то из участков балки поперечная сила есть величина постоянная, то соотношение, полученное для чистого изгиба остается справедливым и для деформации поперечного изгиба: σ=М_х/I_x *y.

Если же поперечная сила на участке изогнутого стержня не является постоянной величиной, то можно показать, что погрешность определения нормальных напряжений по формулам чистого изгиба имеет порядок отношения:

ε~h/l.

Это дает возможность перевести выводы и основные соотношения чистого изгиба на деформацию поперечного изгиба и также можно считать при поперечном изгибе сечения плоскими после изгиба. Это утверждение можно считать настолько приемлемым, насколько угловые деформации из-за сдвига меньше, чем угловые перемещения, обусловленные изменением кривизны бруса. Отличительной особенностью поперечного изгиба является наличие нормальных напряжений. При прямом поперечном изгибе считается, что 1/ρ=±М_х/ЕI_{x –} справедливо как для поперечного изгиба, так и для чистого.