
- •1)Главные площадки и главные напряжения. Виды напряжённого состояния.
- •2) Теории прочности, их назначение. Теория прочности наибольших касательных напряжений. Условие прочности.
- •3) Изгиб. Общие понятия и определения. Виды изгиба. Типы опор и вычисление опорных реакций (пример).
- •4) Внутренние силовые факторы при изгибе. Порядок их определения. Знаки для m,q,n.
- •9) Нормальные напряжения при плоском изгибе (вывод). Распределение напряжений по высоте балки.
- •10) Условие прочности при изгибе по нормальным напряжениям. Виды расчётов на прочность при изгибе.
- •15) Линейные и угловые перемещения при изгибе. Общие понятия. Дифференциальное уравнение изогнутой оси балки (вывод).
- •16) Метод начальных параметров. Определение перемещений в балках с несколькими участками нагружения (пример).
- •17) Теорема о взаимности дополнительных работ внешних сил. Теорема о взаимности перемещений.
- •18) Теорема о взаимности дополнительных работ внутренних сил.
- •19) Интеграл Мора (вывод).
- •20) Порядок определения перемещений при изгибе с помощью интеграла Мора (пример).
- •21) Вычисление интеграла Мора способом Верещагина (вывод). Условия применимости способа Верещагина.
- •22) Порядок определения перемещений способом Верещагина (пример).
- •23) Статически неопределимые системы при изгибе. Выбор основной системы. Эквивалентная система.
- •24) Канонические уравнения метода сил.
- •25) Основные этапы расчёта статически неопределимых балок методом сил (привести пример).
- •26) Основные этапы расчёта статически неопределимых рам методом сил (привести пример).
- •27) Определение перемещений в статически неопределимых системах (привести пример).
- •28,29) Особенности расчёта симметричных статически неопределимых рам с кососимметричной и симметричной нагрузкой (привести пример).
- •30) Сложное сопротивление. Косой изгиб. Определение напряжений и положение нейтральной оси. Условие прочности.
- •31) Сложное сопротивление. Косой изгиб. Определение перемещений.
- •32) Совместное действие изгиба си кручения. Определение напряжений и диаметров вала по III или IV теориям прочности.
- •33) Внецентренное растяжение или сжатие. Определение напряжений и положения нейтральной оси. Условие прочности.
- •34)Расчёты на прочность при напряжениях, циклически изменяющихся во времени. Механизм усталостного разрушения. Параметры цикла.
- •35) Предел выносливости. Экспериментальное определение предела выносливости при симметричном цикле нагружения.
- •36) Определение предела выносливости для асимметричных циклов напряжений с помощью диаграммы максимальное – среднее напряжение.
- •37) Факторы, влияющие на предел выносливости, их количественная оценка.
- •38) Определение коэффициента безопасности (запаса прочности) при циклически изменяющихся напряжениях (изгиб, кручение, изгиб с кручением).
- •39) Расчёты сжатых стержней на устойчивость. Общие понятия. Формы равновесия.
- •40) Формула Эйлера для критической силы (вывод).
15) Линейные и угловые перемещения при изгибе. Общие понятия. Дифференциальное уравнение изогнутой оси балки (вывод).

Линейное перемещение центра тяжести поперечного сечения в направлении перпендикулярном перемещению оси балки называется прогибом V(z) – прогиб.
Угол отклонения поперечного сечения от первоначального положения называется углом поворота сечения θ(z) – угол поворота.
Аналитические методы определения перемещений.
![]()
При слабом изгибе
 – Первая производная прогиба = углу
поворота прогиба
– Первая производная прогиба = углу
поворота прогиба
 - Кривизна нейтрального слоя
- Кривизна нейтрального слоя
 – Кривизна произвольной кривой
– Кривизна произвольной кривой
 – Точное
дифференциальное уравнение изогнутой
оси балки
– Точное
дифференциальное уравнение изогнутой
оси балки
При
слабом изгибе

 - Приближённое
дифференциальное уравнение изогнутой
оси
- Приближённое
дифференциальное уравнение изогнутой
оси
Интегрируем (5)
 – Уравнение углов поворота
– Уравнение углов поворота
Интегрируем (6)
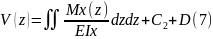 – Уравнение прогибов
– Уравнение прогибов
С и D – постоянные интегрирования определяемые из граничных условий.
16) Метод начальных параметров. Определение перемещений в балках с несколькими участками нагружения (пример).
Назначение: используется для уменьшения постоянных интегрирования.


Правила метода начальных параметров
Начало координат выбирается на одном из концов балки.
Уравнение изгибающих моментов записывается для участка наиболее удалённого от начала координат.
Рассматривается та часть балки, в которой содержится начало координат.
Если распределённая нагрузка прерывается при переходе к следующему участку, она продолжается до конца балки и добавляется в компенсирующую нагрузку.
Интегрирование производится без раскрытия скобок.
Сосредоточенные внешние моменты входят в уравнение изгибающих моментов с фиктивным плечом.
Постоянные интегрирования C и D представляют собой соответственно угол поворота и прогиб в начале координат
Правило знаков для перемещения: положительный прогиб вверг, отрицательный вниз.
Положительный угол поворота против часовой стрелки, отрицательный по часовой при z слева направо.
Условие жёсткости при изгибе.
Vmax
 [V],
[V]=(0.001
[V],
[V]=(0.001 0.001)
0.001)
17) Теорема о взаимности дополнительных работ внешних сил. Теорема о взаимности перемещений.
Теорема. Работа внешних сил первого состояния на перемещение вызванное силами второго состояния равно дополнительной работе внешних сил второго состояния на перемещение вызванное силами первого состояния.


F1Δ12=F2 Δ21 (2) – теорема Бетти
W12=W21 (1)
Если
 – Единичная безразличная сила (фиктивная)
– Единичная безразличная сила (фиктивная)
Из (2) Δ12= Δ21 (3) – Теорема о взаимности перемещений (теорема Максвелла)
Перемещение в направлении первой единичной силы за счёт действия второй единичной силы равно перемещению в направлении второй единичной силы за счёт первой единичной силы.

18) Теорема о взаимности дополнительных работ внутренних сил.

 (a)
(a)
Длина нейтрального
слоя
 ,
после деформации
,
после деформации

т.к.
 (б)
(б)
 dz
dz
(б)
(а)
:

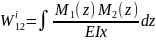 (4) – Дополнительная работа
(4) – Дополнительная работа
 (5)
(5)

По закону сохранения
 (6)
(6)
19) Интеграл Мора (вывод).



 – для изгибающего момента от внешней
нагрузки в заданной системе.
– для изгибающего момента от внешней
нагрузки в заданной системе.
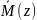 – для изгибающего момента в вспомогательной
системе от единичного усилия
– для изгибающего момента в вспомогательной
системе от единичного усилия
 – Интеграл Мора.
– Интеграл Мора.
Пример.

