14. Определение точки перегиба. Достаточные условия.
Точка (x0;f(x0)) называется точкой перегиба графика функции y=f(x), если в этой точке существует касательная и если она отделяет интервал выпуклости от интервала вогнутости.
Пусть функция y=f(x) дважды дифференцируема в некоторой окрестности точки x=x0, и в точке (x0;f(x0)) существует касательная к графику этой функции. Если при переходе через точку x=x0 вторая производная меняет знак, то точка (x0;f(x0)) является точкой перегиба графика функции.
15. Определение асимптоты к графику функции и нахождение невертикальной асимптоты.
Асимптотой данной кривой называется такая прямая, что расстояние от точки на кривой до этой прямой стремится к нулю при неограниченном удалении этой точки от начала координат.
Наклонные (невертикальные) асимптоты - асимптоты, не параллельные оси oy. Кривая, заданная уравнением y=f(x) имеет невертикальную асимптоту, определяемую уравненем y=kx+b, тогда и только тогда, когда существуют конечные пределы
и
(или соответственно при x-)
Правило Лопиталя
Если функции f(x) и g(x) дифференцируемы в некоторой окрестности точки x=x0 и
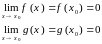
и
, то выполняется равенство
2. Теорема Ролля и ее геометрический смысл.
Если функция y=f(x) непрерывна на отрезке [a;b], дифференцируема в каждой внутренней точке этого отрезка и на его концах обращается в нуль, то внутри отрезка [a;b] найдется такая точка , что f ‘()=0.
Если функция y=f(x) удовлетворяет на отрезке [a;b] всем условиям теоремы Ролля, то на графике функции найдется такая точка, касательная в которой параллельна оси абсцисс.
3. Теорема Лагранжа и ее геометрический смысл.
Если функция y=f(x) непрерывна на отрезке [a;b] и дифференцируема в каждой внутренней его точке, то внутри отрезка [a;b] найдется такая точка , что выполняется равенство
f(b)-f(a)=f ‘()(b-a).
Если функция y=f(x) на отрезке [a;b] удовлетворяет всем условиям теоремы Лагранжа, то на дуге, являющейся графиком этой функции, найдется такая точка, касательная в которой будет параллельна хорде, стягивающей эту дугу.
4. Точки разрыва функции. Их классификация.
Точка x=x0 называется точкой разрыва функции y=f(x), если эта функция не является непрерывной в этой точке.
Точка x=x0 называется точкой разрыва первого рода, если в этой точке существует предел слева и справа от этой функции.
Точка x=x0 называется точкой разрыва второго рода, если хотя бы один из пределов слева и справа не существует.
5. Выпуклость. Вогнутость.
График функции y=f(x) называется выпуклым [вогнутым] в точке (x0;f(x0)), если в этой точке существует касательная к этому графику, которая в некоторой окрестности этой точки расположена выше [ниже] этой кривой.
График функции y=f(x) называется выпуклым [вогнутым] на интервале (a;b), если он выпуклый [вогнутый] в каждой точке этого интервала.
6. Точки перегиба. Достаточное условие.
Точка (x0;f(x0)) называется точкой перегиба графика функции y=f(x), если в этой точке существует касательная и если она отделяет интервал выпуклости от интервала вогнутости.
Пусть функция y=f(x) дважды дифференцируема в некоторой окрестности точки x=x0, и в точке (x0;f(x0)) существует касательная к графику этой функции. Если при переходе через точку x=x0 вторая производная меняет знак, то точка (x0;f(x0)) является точкой перегиба графика функции.