3. Определение касательной и нормали к плоской кривой. Вывод их уравнений.

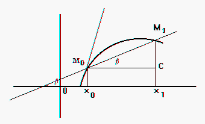
Касательной к данной кривой в данной на ней точке M₀ называется предельное положение секущей при условии, что точка M₁, перемещаясь по этой кривой, неограниченно приближается к точке M₀.

Рассм. M₀CM₁: M₀(x₀;y₀) M₁(x₁,y₁)

tg=M₁C/M₀C M₀C=x₁-x₀=x M₁C=y₁-y₀=y

Нормалью данной кривой в данной на ней точке называется прямая, проходящая через эту точку перпендикулярно касательной в этой точке.

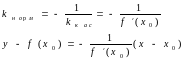
4. Определение непрерывности и дифференцируемости функций. Теорема о связи непрерывности и дифференцируемости.

Функция y=f(x) называется непрерывной в точке x=x₀, если она определена в некоторой окрестности точки x₀ (очевидно, и в самой точке x₀)и если или,что то же самое

Функция y=f(x) называется дифференцируемой в точке x=x₀, если ее приращение в этой точке может быть представлено в виде y=Ax+(x)x, где A=const,

Если функция y=f(x) дифференцируема в точке x=x₀, то она непрерывна в этой точке.

Дано: y=f ‘(x₀)x+(x)x

Док-ть:

Док-во:

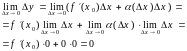
7. Вывод формул для производных sinx, cosx

y=sinx:

x; y=f(x₀+x)-f(x₀)

y=sin(x₀+x)-sinx₀=2sin(x/2)cos(x₀+x/2)

y=cosx:

x; y=f(x₀+x)-f(x₀)

y=cos(x₀+x)-cosx₀=-2sin(x/2)sin(x₀+x/2)

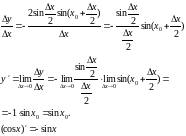
8. Вывод формулы производной сложной функции.

Если функция x=(t) дифференцируема в точке t₀, а функция y=f(x) дифференцируема в точке x=x₀=(t₀), то сложная функция y=f((t)) дифференцируема в точке t=t₀ и ее производная в этой точке находится по формуле

Док-во:

Т. к. функция y=f(x) дифференцируема в точке x=x₀, то y=f ‘(x₀)x+(x)x.

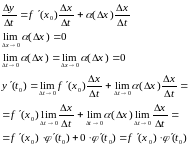
9. Вывод формулы для производной логарифмической функции.

11. Вывод производных показательной и степенной функций.

Производная показательной функции:

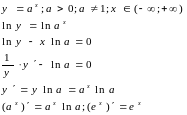
Производная степенной функции:

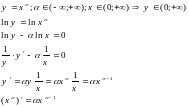
12. Дифференциал функции. Определение. Свойство инвариантности формы дифференциала.

Дифференциалом дифференцируемой функции называется главная, линейная относительно x, часть приращения функции.

Форма дифференциала функции f(x) не зависит от того, является ли x независимой переменной или функцией другого независимого переменного.

Док-во:

13. Определение максимума и минимума. Док-во необходимого условия экстремума.

Функция y=f(x) имеет максимум [минимум] в точке x=x₀, если найдется такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство f(x₀)>f(x) [f(x₀)<f(x)].

Если функция y=f(x) имеет в точке x=x₀ экстремум, то ее производная в этой точке равна 0 или не существует(???).

Дано: x=x₀ -точка максимума.

Док-ть: f ‘(x₀)=0.

Док-во:

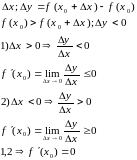
(для минимума - по аналог. док-ву)

14. Определение максимума и минимума. Доказательство достаточных условий экстремума.

Функция y=f(x) имеет максимум [минимум] в точке x=x₀, если найдется такая окрестность этой точки, что для всех x из этой окрестности выполняется неравенство f(x₀)>f(x) [f(x₀)<f(x)].

Если функция y=f(x) непрерывна в точке x=x₀ и дифференцируема в некоторой окрестности этой точки, и если при переходе через эту точку производная меняет знак, то в этой точке функция имеет экстремум: если знак f ‘(x) меняется с “+” на “-” - то функция имеет максимум в этой точке; если с “-” на “+” - то минимум.

Док-во:

Функция f(x) удовлетворяет всем условиям теоремы Лагранжа.