21.Основные газовые законы и область их применения. Идеальный газ. Выводы закона Клапейрона-Менделеева. Универсальная газовая постоянная.

Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют малые собственные размеры. Это идеализированная модель, согласно которой:

1. Собственный объём молекул газа пренебрежимо мал по сравнению с объёмом сосуда;

2. Между молекулами газа отсутствуют силы взаимодействия;

3. Столкновение молекул газа между собой и со стенками сосуда абсолютно упругие.

Уравнением Клайперона называется соотношение, справедливое для постоянной массы идеального газа: . R=C\v – молярная газовая постоянная, согласно закону Авогадро (при одинаковых давлениях и температурах молярные объемы различных газов также одинаковы). Отсюда следует, что R одинаково у всех газов. Поэтому ее принято называть универсальной газовой постоянной. R = 8, 31 Дж/(K  моль)

Молярной массой любого тела называется физическая величина, равная отношению массы тела к количеству  молей, которое в нём содержится:  = m/,   = m/ ;  = 10 ^–3  m/m_o , где m  масса молекулы данного тела, m_o  масса одной двенадцатой массы атома углерода.

Молярным объёмом называется физическая величина, равная отношению объёма газа к числу молей, содержащихся в газе: V_ =V/ .

Вывод уравнения Менделеева – Клайперона.

V_ =V/, перепишем уравнение состояния в форме учтя что R=C\, получим P V_ = RT отсюда PV = RT.

22.Вывод основного уравнения молекулярно кинетической теории газов для давления. Средняя квадратичная скорость молекул. Средняя кинетическая энергия поступательного движения молекул газа.

Основным уравнение кинетической энергии газов есть соотношение: .

Это уравнение выполняется при N = const  общее число молекул в газе, то есть при отсутствии химических реакций; газ может состоять из разнородных молекул.

 суммарная энергия поступательного движения молекул газа, находящихся в сосуде, где m_i  масса, а V_i  скорость «i  ой» молекулы.

Для однородного газа m_i = m_o , тогда .

Средняя кинетическая энергия поступательного движения молекул газа.

Введём средне квадратичную скорость V _квадр. поступательного движения молекул газа: . Тогда

Подставим данный результат в основное уравнение кинетической теории газов

(*), m  масса всего газа.

Сопоставим полученный результат с уравнением МенделееваКлайперона:

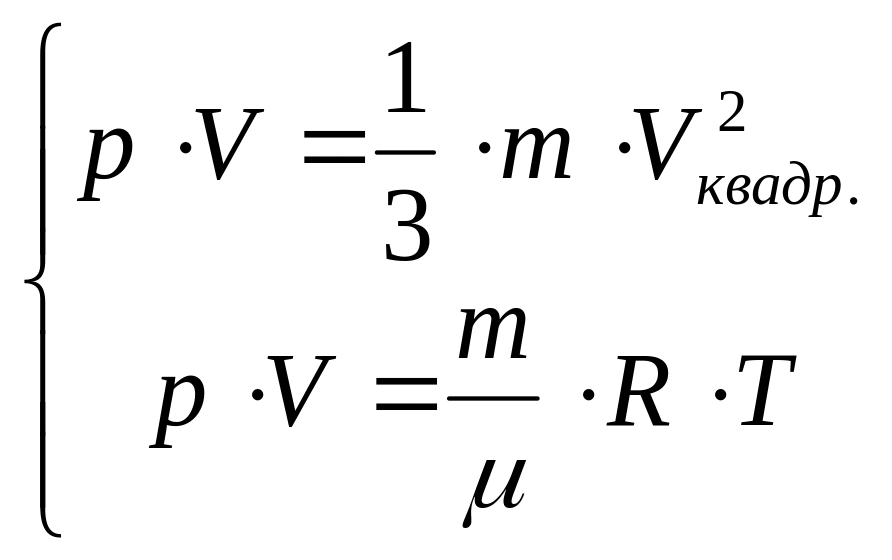
, здесь использовалось полезное соотношение: . Связь давления, плотности газа и средней квадратичной скорости следует (*):

Средняя кинетическая энергия поступательного движения одной молекулы идеального газа:

.После подстановки явного выражения для средней квадратичной скорости, получим:

Наиболее вероятная скорость v_B – соответствует максимуму f.

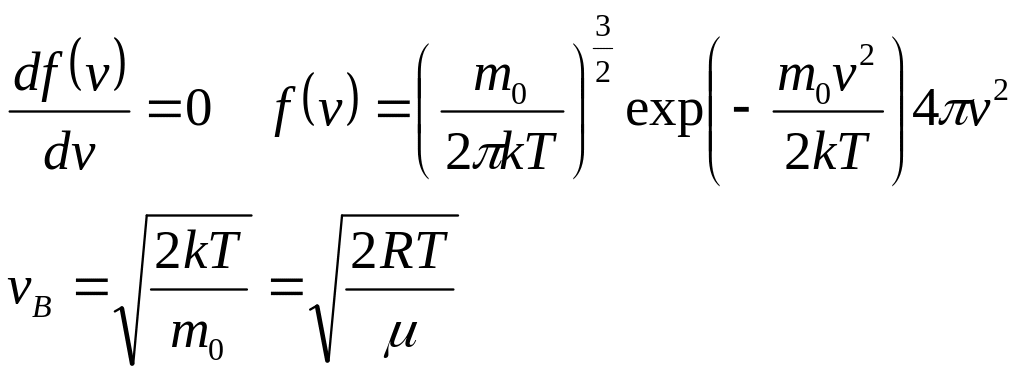
23.Распределение скоростей молекул по Максвеллу. Наиболее вероятная скорость, средняя арифметическая скорость. Опыт Штерна.

Закон распределения молекул идеального газа по скоростям определяет долевое участие молекул однородного газа в тепловом движении при данной температуре со скоростями, заключёнными в интервале от V до V + V. Он выведен теоретически: ,

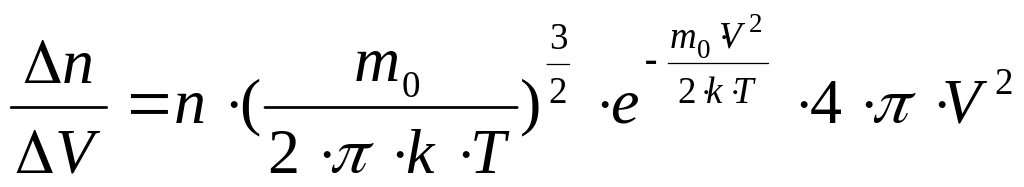где n  число молекул в единице объёма (концентрация молекул),

n  число молекул из общего их числа, скорости которых лежат в интервале скоростей: ,

m₀  масса одной молекулы,

k  постоянная Больцмана,

T  температура газа.

Чем меньше по величине выбирается интервал скоростей, тем более точный результат даёт данная формула.

N в единицу объёма, которые [,+ ]

Графическая иллюстрация данной формулы приведена на графике зависимости относительной концентрации молекул n/V идеального однородного газа от скорости.Функцией распределения молекул идеального газа по скоростям Максвелла называется выражение: .С помощью этой функции можно найти все статистически необходимые величины, характеризующие состояние идеального газа.

Вначале найдём наивероятнейшую скорость, т.е. значение скорости, соответствующее максимуму функции Максвелла. С точки зрения физики  это такое значение скорости, к которому близки значения скорости большей части молекул. Воспользуемся методом нахождения экстремума функции, т.е. вначале возьмём производную от функции распределения Максвелла по скорости, а затем приравняем полученное выражение к нулю:

.

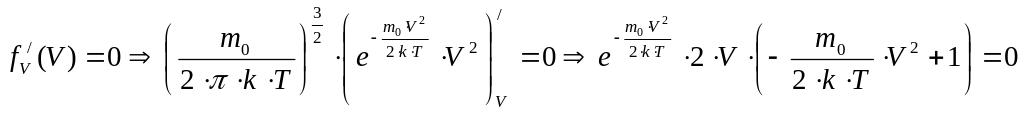Последнее уравнение имеет три решения, т.к. необходимо равенство нулю каждого из множителей: