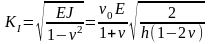- •Билет 1
- •Билет 2
- •Билет 3
- •Билет 4
- •Билет 5
- •Билет 6
- •Наклонная трещина в одноосном поле напряжений
- •Билет 7
- •Распределение напряжений вблизи вершины трещины
- •Билет 8
- •Антиплоская деформация
- •Билет 9
- •Билет 10
- •Критерий Райса
- •Билет 11
- •Подборка точных решений.
- •Взаимодействие трещин
- •Графики и ) Приближенные значения кин
- •Принцип суперпозиции для нахождения кин трещин.
- •Билет 12
- •Билет 13
Билет 10
Критерий Новожилова.
Критерий
Новожилова применяется для определения
критических нагрузок для тел с трещинами,
вырезами, выточками и другими
концентраторами. Напряжения вблизи
концентратора усредняются по некоторому,
характерному для данного материала
интервалу
и сравниваются с величиной прочности
тела .
По Новожилову прочность тела сохраняется,
если в любой точке тела
.
По Новожилову прочность тела сохраняется,
если в любой точке тела
 .
(29)
.
(29)
Здесь
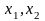 -
главные оси тензора напряжений. Для
трещин интервал
берется у вершины трещины на ее
продолжении. Там
-
главные оси тензора напряжений. Для
трещин интервал
берется у вершины трещины на ее
продолжении. Там
 ,
подставляя это выражение для напряжений
в критерий, получаем условие устойчивости
трещины:
,
подставляя это выражение для напряжений
в критерий, получаем условие устойчивости
трещины: .
Это условие аналогично критерию Ирвина.
Критерий Новожилова более универсален.
Он работает на разных концентраторах
и на однородном поле напряжений.
.
Это условие аналогично критерию Ирвина.
Критерий Новожилова более универсален.
Он работает на разных концентраторах
и на однородном поле напряжений.
Интеграл Райса и его связь с удельной энергией разрушения.
Критерий Райса
Эшелби,
Райс и Черепанов ввели в рассмотрение
применительно к трещинам независящий
от пути интегрирования контурный
интеграл. Его контур интегрирования
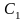 начинается
на одном берегу трещины, охватывает
вершину и заканчивается на другом берегу
(рис.5).
начинается
на одном берегу трещины, охватывает
вершину и заканчивается на другом берегу
(рис.5).
 Рис.5
Рис.5
 (30)
(30)
Здесь
 -
плотность упругой энергии,
-
плотность упругой энергии,
 -
вектор сил на площадке с нормалью
-
вектор сил на площадке с нормалью
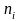 .
Для упругого изотропного тела
.
Для упругого изотропного тела

При
этом

В
общем случае

Введем
еще контур
 .
Интеграл (30) по нему равен
.
Интеграл (30) по нему равен
 .
Рассмотрим составной контур
.
Рассмотрим составной контур
 .
На свободных от напряжений берегах
вклад в интеграл равен нулю, так как
.
На свободных от напряжений берегах
вклад в интеграл равен нулю, так как
 ,
поэтому интеграл по контуру
,
поэтому интеграл по контуру
 :
:
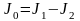 .
Знак – объясняется тем, что интеграл
по
берется
в обратном направлении.
.
Знак – объясняется тем, что интеграл
по
берется
в обратном направлении.
Покажем,
что интеграл по контуру
равен
нулю. Для интеграла от первого слагаемого
в (30) справедлива формула Грина, по
которой интеграл по контуру можно
привести к интегралу по площади.
по контуру
равен
нулю. Для интеграла от первого слагаемого
в (30) справедлива формула Грина, по
которой интеграл по контуру можно
привести к интегралу по площади.
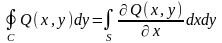 .
(31)
.
(31)
Здесь S – площадь односвязной области, ограниченной контуром С.
Интеграл от второго слагаемого приводится к интегралу по площади с помощью формулы Остроградского – Гаусса:
 .
(32)
.
(32)
В
(30) вектор сил на площадке с нормалью
определяется по тензору напряжений по
формуле:
 .
С учетом этого второе слагаемое в (30)
равно:
.
С учетом этого второе слагаемое в (30)
равно:
 .
.
Отсюда
вектору
 в
(32) в (39) соответствует
в
(32) в (39) соответствует
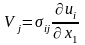 .
Вычислим
.
Вычислим
 :
:

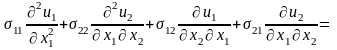
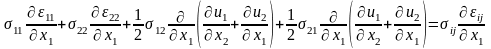 .
.
Объединяя все части интеграла (30) по контуру , получаем:
 . (33)
. (33)
Проведем дифференцирование плотности упругой энергии.
 .
.
Подставляя
полученное выражение в (33), получаем
 .
.
Отсюда следует, что интеграл Райса (30) не зависит от пути интегрирования. Физический смысл этой величины можно понять из следующих расчетов. Возьмем контур интегрирования в (30) достаточно близко к вершине трещины, чтобы можно было пользоваться асимптотическим полем деформаций, которое существует около вершины.
Дадим небольшое приращение трещине, так что ее вершина переместится на . Рассчитаем на сколько изменится энергия внутри контура . Эта энергия равна работе сил на контуре на перемещениях, возникших при подрастании трещины. Перемещения вблизи вершины трещин описываются соответствующим асимптотическим законом:
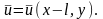 Изменение
перемещений равно
Изменение
перемещений равно
 .
При этом работа сил
.
При этом работа сил
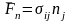 ,
действующих на площадках, касающихся
контура
(
,
действующих на площадках, касающихся
контура
( -вектор
нормали к контуру), определяется
величиной:
-вектор
нормали к контуру), определяется
величиной:

Передвинем контур вдоль оси Х на . Энергия среды внутри контура изменится из-за входа и выхода точек среды с плотность внутренней энергии . Такое изменение можно рассчитать через контурный интеграл:

 .
.
Объединяя
слагаемые
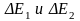 ,
получим, что изменение энергии среды
внутри контура
,
когда он перемещается вместе с вершиной
трещины
,
получим, что изменение энергии среды
внутри контура
,
когда он перемещается вместе с вершиной
трещины

Отсюда
следует, что интеграл Райса
равен
удельной энергии
,
которая может пойти на подрастание
трещины. Согласно (24) получаем связь
коэффициентов интенсивности с
.
В случае нормального разрыва и плоской
деформации имеем
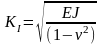
В равновесном состоянии:
 по
критерию Гриффитса, и
по
критерию Гриффитса, и
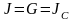 по Ирвину.
по Ирвину.
Из
последнего равенства следует:

В расчетах удобно определять , подбирая нужным образом контур интегрирования.
Как пример,
рассмотрим задачу о полубесконечной
трещине в полосе, которая растягивается
в поперечном направлении. Рассмотрим
случай, когда края полосы расходятся
на постоянную величину
 . Построим контур интеграла Рейса вдоль
краев полосы( участки
. Построим контур интеграла Рейса вдоль
краев полосы( участки
 и
и
 )
и вдоль поперечных отрезков
)
и вдоль поперечных отрезков
 и
. Причем такие отрезки возьмем достаточно
далеко от вершины трещины, так чтобы
напряженное состояние в окрестности
отрезков мало отличалось от предельного
значения напряженного состояния при
и
. Причем такие отрезки возьмем достаточно
далеко от вершины трещины, так чтобы
напряженное состояние в окрестности
отрезков мало отличалось от предельного
значения напряженного состояния при
 .
.
Интегралы вдоль
горизонтальных участков
и
равны нулю, так как на них
 .
Интеграл по отрезку
равен нулю, так как в области над разрезом
далеко от вершины трещины среда разгружена
полностью и там
.
Интеграл по отрезку
равен нулю, так как в области над разрезом
далеко от вершины трещины среда разгружена
полностью и там
 .
.
На
отрезке
имеем
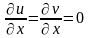 .
Отсюда следует, что второе слагаемое в
интеграле Райса равно нулю и, окончательно
имеем:
.
Отсюда следует, что второе слагаемое в
интеграле Райса равно нулю и, окончательно
имеем:
 ,
где
-
ширина полосы. Остается выразить
,
где
-
ширина полосы. Остается выразить
 через заданные параметры задачи
через заданные параметры задачи
 .
.
Воспользуемся законом Гука, записанным через модуль Юнга и коэффициент Пуассона.
 .
.
Отсюда

Рассмотрим
случай плоского деформированного
состояния:
 .
Так как вдоль полосы
.
Так как вдоль полосы
 ,
имеем
,
имеем
 .
В итоге
.
В итоге
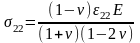 ,
,
 .
.
 .
.
Отсюда
имеем: