Билет 9

1. Эксперементальные методы определения КИН.

2. Численный метод разрывных смещений. Решение задачи о прямолинейной дислокации отрыва.

Метод разрывных смещений ориентирован в первую очередь на определение напряженного состояния тел с трещинами. Каждая трещина разбивается по длине на большое число отрезков, в пределах которых нормальное раскрытие и тангенциальный сдвиг усредняются. Напряженное состояние тела с трещиной представляется как сумма полей, вызванных получающимися раскрытиями и сдвигами всех отрезков трещины. Основой метода являются поля напряжений и деформаций в упругой плоскости, возникающие в ней при единичном однородном раскрытии и сдвиге на прямолинейном отрезке. Поле исходной задачи строится как суперпозиция таких полей с неизвестными заранее величинами раскрытий и сдвигов. Требование выполнения граничных условий на трещине позволяет построить систему линейных уравнений относительно неизвестных скачков смещений и сдвигов. Решение этой системы позволяет определить поля напряжений и деформаций в любой точке плоскости.

Рассмотрим задачу о нормальном разрыве на отрезке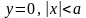

Обозначим смещения верхнего берега разрез, как и 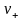и нижнего, как и .

Мерой разрыва смещений введем и

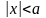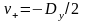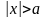
Будем считать, что на интервале нормальный разрыв постоянен и равен . При этом на верхнем берегу разреза . При и в силу симметрии задачи всюду 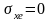. Из последнего следует следующее представлений напряжений и смещений через функцию комплексного переменного:

,

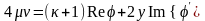
Отсюда 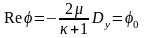при . При : .

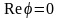В итоге, для верхней полуплоскости имеем задачу Дирихле, когда на границе области задана реальная часть функции комплексного переменного. Решением такой задачи является интеграл Шварца для полуплоскости.

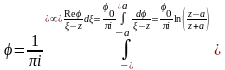
Проверим выполнение граничных условий.

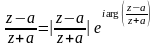. С учетом этого .

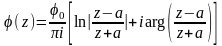Отсюда , где и

У

0

a

-a

z-a

z+a

z

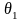z

z

глы и приведены на рисунке.

Из рисунка следует и . Легко видеть, что пр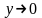и и : , а при : , что и требуется.

Итак, , ,

Подставим это в выражение для напряжения : .

Вычислим отдельные слагаемые:

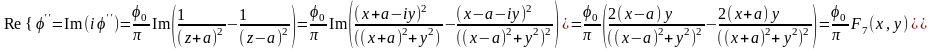
В итоге, .

При ,

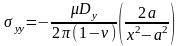
Покажем, как это решение может быть использовано для численного решения задачи о равновесии прямолинейного разреза, нагруженного изнутри. Для этого разделим разрез по длине на 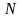отрезков, каждый из которых представляется как элементарный разрыв смещения . Тогда численная аппроксимация задачи может быть представлена разрывами смещений 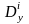( 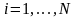). Значения этих разрывов определяются при решении системы уравнений, полученных из условия соответствия граничных напряжений на берегах разреза нагрузке 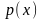, приложенной к ее берегам в центрах отрезков. Если разрыв имеет место на отрезке длиной с центром в точке , , то напряжение от этого разрыва на оси х определяются формулой:

.

В центре 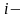того элемента напряжение от того разрыва будет равно:

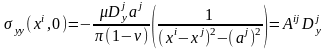, где 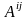- коэффициент влияния того элемента на тый.

Согласно принципу суперпозиции напряжение в центре того элемента от всех разрывов будет равно:

. Второе равенство следует из выполнения граничного условия.

Решение получившейся системы уравнений позволяет найти неизвестные . По можно найти все поля. Для определения КИН можно использовать особые элементы для описания раскрытия вершин трещин. На этих элементах раскрытие не постоянное, а изменяется по параболическому закону, что характерно для раскрытия у вершин трещин.