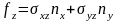Билет 7

1. Антиплоское состояние упругого тела. Уравнения равновесия и граничные условия

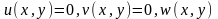- антиплоское состояние.

При антиплоской деформации упругого тела отлична от нуля только компонента и компоненты тензора деформаций:

и

При этом отличны от нуля компоненты тензора напряжений:

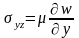, (6)

Уравнение равновесия в отсутствии внешних сил одно:

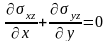или в перемещениях:

, то есть перемещение удовлетворяет уравнению Лапласа и является гармонической функцией.

Граничные условия антиплоской задачи:

1. 

2. 

Наглядное представление о смещениях при антиплоской деформации дает пример сдвигания листов в стопке бумаги ( ось Z ориентирована по направлению сдвига)

2. Угловое распределение напряжения у вершины трещины отрыва (вывод)

Распределение напряжений вблизи вершины трещины

Найдем, используя полученное решение угловое распределение напряжений вблизи вершины трещины нормального отрыва. Пусть 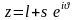, . При этом 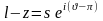. Из (19¹) следует

.

Для того, чтобы найти напряжения при , надо согласно (17) найти . Из (19¹) : . (22)

Так как , где 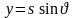, то в выражении (22) для определения главного члена в ассимптотике нам нужно второе слагаемое порядка : .

В итоге имеем:

Вводя коэффициент интенсивности , получаем:

. Аналогично из 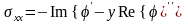и 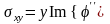можно получить:

,

Для плоской деформации:

При

Максимальные касательные напряжения:

;

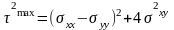Изолинии максимальных касательных напряжений

Билет 8

1. Постановка и решение задачи о прямолинейном разрезе, нагруженного изнутри сдвигающими усилиями, вызывающими антаплоские деформации.

Антиплоская деформация

Вернемся к нашим упругим задачам. Рассмотри для начала случай антиплоской деформации, при котором смещение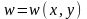 является гармонической функцией. При этом остальные компоненты вектора смещения и определяемые ими напряжения равны нулю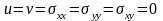 . Пусть имеется разрез вдоль оси X от -l до l. На обоих берегах разреза зададим сдвиговое усилие , вызывающее напряжение 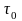: 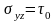. Требуется найти аналитическую функцию , реальная часть которой равна смещению , соответствующему заданным граничным условиям.

Из соображений симметрии напряжения симметричны относительно оси X, а смещения w и напряжения антисимметричны. Поэтому на продолжении разреза . Рассмотрим верхнюю полуплоскость. На ее границе имеем при 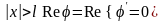.Введем в рассмотрение . Отсюда

при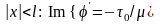 . Кроме этого будем искать решение непрерывное по перемещению в вершинах разреза и убывающее на бесконечности.

В итоге, для имеем смешанную задачу: при задано 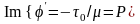, на остальной границе полуплоскости известно, что .

Решение такой задачи дает формула Келдыша-Седова.

(11)

Проведем интегрирование при :

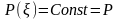Рассмотрим , как функцию комплексных переменных 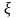и

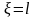Пусть . Проведем разрез плоскости между точками и . Выберем ветвь функции положительной на верхнем берегу разреза. Тогда 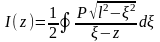. Контурный интеграл берется по контуру вокруг разреза, проходимому по часовой стрелке. Путь интегрирования деформируется в контур вокруг точки (против часовой стрелки) и в бесконечно удаленной точке (по часовой стрелке). Интеграл по равен Интеграл по равен

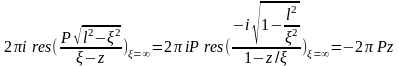
Множитель обусловлен выбором ветви, вычет в бесконечности равен коэффициенту при 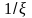с обратным знаком

В итоге:

(12)

Отсюда видно, что при y=0 и -l<x<l 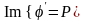, при

Интегрируя (12), имеем

.

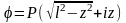Это решение справедливо во всей плоскости с разрезом. Радикал положителен при .

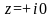Найдем смещения при у=0 и -l<x<l:

Верхний берег разреза смещается за плоскость Z=0, нижний выступает вперед. При этом 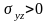и сверху и снизу.

Сдвиговые напряжения при у=0 и определяются формулой:

Значения функци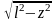и на оси

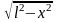
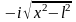
Отсюда при , при

-l 0 l

Напряжения стремятся к 0 при При имеем:

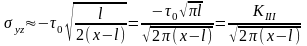, отсюда

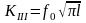
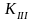-коэффициент интенсивности напряжений в вершине трещины при антиплоском деформировании, - нагрузка на верхнем берегу разреза ( ).

Определим распределение напряжений у вершины трещины.

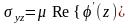
Вблизи вершины и

. Знак в этой формуле выберем из условия, что на верхнем берегу разреза при 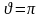: . В этом случае

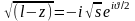
При

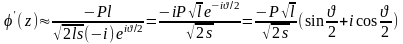
Отсюда следует: ,

2. Экспериментальные методы податливости определения КИН.