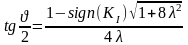- •Билет 1
- •Билет 2
- •Билет 3
- •Билет 4
- •Билет 5
- •Билет 6
- •Наклонная трещина в одноосном поле напряжений
- •Билет 7
- •Распределение напряжений вблизи вершины трещины
- •Билет 8
- •Антиплоская деформация
- •Билет 9
- •Билет 10
- •Критерий Райса
- •Билет 11
- •Подборка точных решений.
- •Взаимодействие трещин
- •Графики и ) Приближенные значения кин
- •Принцип суперпозиции для нахождения кин трещин.
- •Билет 12
- •Билет 13
Билет 6
Плоское состояние упругого тела. Уравнения равновесия и граничные условия.
 - плоское состояние
- плоское состояние
При плоской деформации имеем:
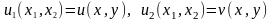 ,
,
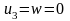
Отсюда из (2) следует:
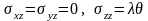 ,
,
где объемное
расширение
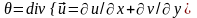
Ненулевые компоненты тензора деформаций имеют вид
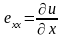

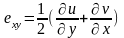
Ненулевые компоненты тензора напряжений:


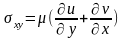
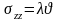 ,
,
где
 (4)
(4)
В случае плоского
напряженного состояния (пластина со
свободными гранями) предполагается,
что, .
Отсюда из (2) следует
.
Отсюда из (2) следует
 и
и
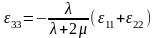
Исключая
 из (2), получаем
из (2), получаем

Из сравнения с (4)
следует, что в случае с плоским напряженным
состоянием в законе Гука параметр
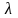 заменяется
на
заменяется
на
 .
.
В случае плоского
состояния из (4) при отсутствии массовых
сил имеем в переменных
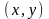 уравнения
равновесия:
уравнения
равновесия:


Для завершения
постановки задачи необходимо выписать
граничные условия на границе области
занятой упругим телом. На границе могут
быть заданы компоненты вектора
поверхностных сил, приложенных к границе
 (первая
краевая задача) или смещений
(первая
краевая задача) или смещений
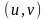 (вторая
краевая задача). В смешанной задаче
теории упругости на одних участках
границы задаются силы на других -
смещения.
(вторая
краевая задача). В смешанной задаче
теории упругости на одних участках
границы задаются силы на других -
смещения.
Компоненты
поверхностных сил ( )
связаны с тензором напряжений и нормалью
)
связаны с тензором напряжений и нормалью
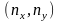 к
границе следующим образом:
к
границе следующим образом:
 или
или

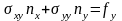 (5)
(5)
Наклонная трещина в поле одноосного растяжения. Определение КИН и направления дальнейшего развития трещины (формула).
Наклонная трещина в одноосном поле напряжений
Применим
метод суперпозиции к решению задачи о
напряженном состоянии наклонной
прямолинейной трещины со свободными
берегами, находящейся в растянутой на
бесконечности упругой плоскости. Пусть
плоскость растянута вдоль оси Y
напряжением
.
Линия трещины составляет угол с
осью Y.
Искомое поле
представим как сумму поля 1 растянутой
плоскости без разреза и поля 2 плоскости,
свободной на бесконечности с разрезом
нагруженным изнутри. Напряженное
состояние поля 1 определяется выражениями:
с
осью Y.
Искомое поле
представим как сумму поля 1 растянутой
плоскости без разреза и поля 2 плоскости,
свободной на бесконечности с разрезом
нагруженным изнутри. Напряженное
состояние поля 1 определяется выражениями:
 ,
,
 .
Найдем вектора напряжений, с которыми
верхний берег линии, где расположен
разрез действуют на нижний. Эти компоненты
вектора определяются через тензор
напряжений и углы внешней нормали к
нижнему берегу линии разреза:
.
Найдем вектора напряжений, с которыми
верхний берег линии, где расположен
разрез действуют на нижний. Эти компоненты
вектора определяются через тензор
напряжений и углы внешней нормали к
нижнему берегу линии разреза:
 ., где
., где
 .
Отсюда
.
Отсюда
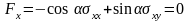
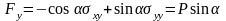 .
.
Вектор
(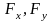 )
разложим на нормальную и тангенциальную
компоненты относительно линии разреза:
)
разложим на нормальную и тангенциальную
компоненты относительно линии разреза:
 ,
,
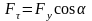 .
Такие усилия, но в противоположном
направлении надо приложить в задаче,
определяющей поле 2. Это выполнится,
если нагрузить берега трещин давлением
.
Такие усилия, но в противоположном
направлении надо приложить в задаче,
определяющей поле 2. Это выполнится,
если нагрузить берега трещин давлением
 и сдвигающим напряжением
и сдвигающим напряжением
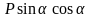 .
Такая нагрузка дает следующие значения
КИН:
.
Такая нагрузка дает следующие значения
КИН:
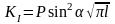 ,
,

Возникают вопросы при каком напряжении растяжения пространства с трещиной, она начнет расти и в каком направлении.
Развитие трещины в условиях отрыва и поперечного сдвига.
Экспериментальные
исследования развития трещин, испытывающих
деформации отрыва и поперечного сдвига
показали, что достаточно хорошо работает
модель обобщенного нормального разрыва.
Согласно этой модели трещина развивается
по радиусу из ее вершины, на котором
максимальны поперечные растягивающие
усилия. Происходит это, когда КИН в этом
направлении равен его критической
величине. Для определения зависимости
угла поворота трещины от значений КИН
-
и
 воспользуемся формулами асимптотического
распределения напряжений у вершины
трещины. Направим ось Х по касательной
к трещине в ее вершине и поместим вершину
в начало координат. Тогда для трещины
отрыва имеем:
воспользуемся формулами асимптотического
распределения напряжений у вершины
трещины. Направим ось Х по касательной
к трещине в ее вершине и поместим вершину
в начало координат. Тогда для трещины
отрыва имеем:
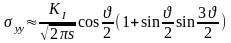 .
.
 ,
,

Эти
формулы позволяют рассчитать компоненты
тензора напряжения для точек любого
радиуса, выходящего из вершины в системе
координат (X,
Y)
под углом
 .
Для расчета напряжений в таких точках
в системе координат, направленных по
радиусу и нормали к нему, можно
воспользоваться формулами преобразования
компонент тензора при повороте системы
координат на угол
:
.
Для расчета напряжений в таких точках
в системе координат, направленных по
радиусу и нормали к нему, можно
воспользоваться формулами преобразования
компонент тензора при повороте системы
координат на угол
:



На
радиусе с максимальными значениями
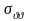 выполняется условие
выполняется условие
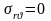 .
Воспользуемся этим условием для
определения направления развития
трещины.
.
Воспользуемся этим условием для
определения направления развития
трещины.
Из приведенных формул следует

Аналогично можно получить для поперечного сдвига:
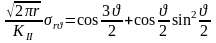
В итоге имеем
 .
.
Преобразуем

Подставляя это выражение, получаем:

После преобразования имеем уравнение для определения :

Выразим
 и
и
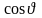 через
через
 .
.
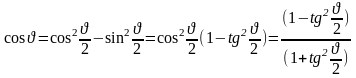
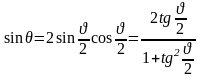
Подставляя эти выражения в уравнении для , получаем:
 ,
где
,
где
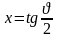
Для
 получаем
квадратное уравнение;
получаем
квадратное уравнение;

Его
решение:
 ,
учитывая, что при
,
учитывая, что при
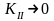
 выбираем знак ( - ) перед корнем.
выбираем знак ( - ) перед корнем.
Введем
 ,
тогда
,
тогда