Билет 5

1. Критерий Гриффитса. Условие равновесного состояния прямолинейной трещины в поле растяжения. Экспериментальная проверка (Гриффитс).

Гриффитс в своих работах объяснил расхождение теоретических оценок прочности кристаллических тел с найденными экспериментально значениями влиянием микротрещин. При этом он указал, как рассчитать предельное состояние тела с трещинами под нагрузкой. Он использовал энергетический подход и постулировал, что на образование новых поверхностей за счет роста трещины необходимы затраты энергии. При увеличении на площади трещины дополнительная работа внешних сил идет на увеличение упругой энергии тела и поверхностной берегов трещин:

, .

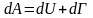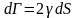Если при виртуальном увеличении трещины высвобождающейся энергии хватает на затраты по образованию новой площади, то трещина будет развиваться, в противоположном случае роста трещины не будет. Такое условие равновесия трещины Гриффитс в случае плоского деформирования сформулировал в виде неравенства

,

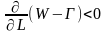где 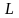- длина трещины

Пусть внешние силы, действующие на тело, занимающее область , - вектор перемещений точек тела,

Энергию 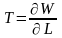, высвобождающуюся при единичном приращении длины трещины, можно записать в виде:

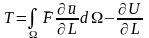(1)

Если при виртуальном увеличении трещины 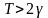, то трещина будет развиваться. В противоположном случае роста трещины не будет.

Высвобождение энергии при росте трещины можно увидеть на простом примере. Рассмотрим растянутую полосу с закрепленными в дальнейшем краями. Если ее медленно разрезать в поперечном направлении, то запасенная в полосе энергия будет исчезать, силы, действующие на зажимы, уменьшатся. Так как тело упругое, то высвобождающая энергия может поглощаться только в вершине трещины, где и происходит разрыв материала.

Рассмотрим два способа вычисления

Пусть внешние силы расположены вне некоторой окрестности у вершины трещины. В положении равновесия наложим на тело жесткие связи там, где приложены внешние силы. Тогда при единичном удлинении трещины выделится энергия

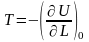, (2)

Где символом обозначена производная упругой энергии при замороженных связях, когда внешние силы не работают.

Пусть теперь связи на силы не накладываются. Тогда для фиксированной трещины при ее нагружении в силу линейности задачи имеем:

,

где поле перемещений зависит от длины трещины . Докажем это. Перейдем от ненагруженного состояния к нагруженному линейно по времени. Пусть в каждой точке, где приложены силы 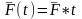( 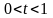), Тогда, в силу линейности: 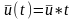. Работа, совершенная внешними силами, перейдет в упругую энергию:

Предположим, что силы не меняются при удлинении трещины (мягкое нагружение). Тогда

Возвращаясь к выражению (1) для , получим:

(3)

Покажем, что правые части формул (2) и (3) равны друг другу. Начальные состояния до вариации трещин в рассматриваемых случаях одинаковы. Состояние после вариации длины трещины во втором случае можно получить из первого, заменив связи их реакциями и увеличив затем последние до первоначальных значений внешних сил. При этом работа внешних сил и упругая энергия деформации получат одно и тоже приращение. И, следовательно, высвободившаяся энергия (2) не изменится. Таким образом, высвобождающаяся энергия равна уменьшению упругой энергии деформации тела в условиях, когда при вариации длины трещины внешние силы не работают, или увеличению упругой энергии (равной половине работы внешних сил) в условиях, когда при той же вариации на тело не накладывается никаких дополнительных связей.

В своей статье Гриффитс рассмотрел прямолинейную трещину длиной 2l , находящуюся в бесконечной плоскости, растягиваемой внешним напряжением в перпендикулярном к плоскости трещины направлении.

При расчетах Гриффитс воспользовался решением задачи о растянутой плоскости с эллиптическим вырезом. Мы воспользуемся решением задачи о равновесии разреза длиной 2l в плоскости, растянутой напряжением P. Согласно этому решению известна форма берегов разреза:

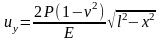. (4)

Используя это выражение можно найти величину высвободившейся энергии растянутой пластины при появлении в ней трещины. Рассмотрим последовательно переход из напряженного состояния растянутой плоскости без разреза к плоскости с разрезом. Введем согласно рис.2 состояния 0-3.

Рис. 2. Последовательные состояния растянутой плоскости при раскрытии в ней трещины.

Переход из состояния 0 в 1 не меняет энергию упругой плоскости. При переходе из 1 в 2 такое изменение происходит. Для расчета изменения надо перейти от 1 к свободному от нагрузок разрезу (состояние 2) постепенно уменьшая растягивающее напряжение, приложенное к его берегам от значения P до 0 . Графики раскрытия разреза в разных его точках от напряжения P приведены на рис.3. При этом будет совершена работа, определяемая площадью под этим кривыми

Рис.3 Уменьшение напряжения на берега разреза при его раскрытии до состояния свободной от напряжения трещины в разных ее точках

(5)

Получаем, что уменьшение упругой энергии при переходе из состояния 1 в 2 равно . Отсюда и из (2) следует

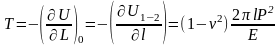
Заметим здесь, что переход из состояния (2) в (3) (рис.2), которое можно совершить заменяя связи силами и затем увеличивая их до положенного значения, не приводит к выделению энергии, так как вся работа переходит в упругую энергию.

В рассматриваемом случае условие равновесного состояния трещины является: , так как трещина удлиняется симметрично вправо и влево по оси .

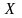Учитывая это из (6) следует:

- критическая нагрузка, превышение которой приводит к неограниченному росту трещины.

Из приведенной для критической нагрузки формулы следует:

(3)

Это соотношение Гриффитс проверял экспериментально, разрушая внутренним давлением стеклянные полые шары и трубки. Предварительно в стекле создавались трещины разной длины. В эксперименте фиксировалось давление, при котором происходило разрушение. Результаты приведены для шаров в таблице 1

2l, inch	D, inch	P, lbs.per sq/inch
0.15	1.49	864	237
0.27	1.53	623	228
0.54	1.60	482	251
0.89	2	366	244

Экспериментально для исследуемого стекла Гриффтс определил значение поверхностной энергии, как 0.0031 lbs. per inch =0.0031*4.45N/0.025=0.55Н/m. Это значение было получено экстраполяцией данных о поверхностной энергии жидкого стекла при снижении температуры расплава. Расчет по формуле (3) для значений параметров стекла дает =266. Это замечательное согласие с экспериментом.

В последствии многими экспериментами была подтверждена теория Гриффитса, были разработаны методики определения для конструкционных материалов, и для многих материалов она была найдена. Это позволяет расчетами определять уровень безопасных нагрузок в конструкциях, содержащих трещины. Для проведения таких расчетов надо уметь находить напряженное состояние упругих тел под нагрузкой при наличии в них трещин.

2. Равновесие трещин в балочном приближении. Локальный и энергетический критерий .

В задачах о расщеплении тонких полос и пластин можно использовать балочное приближение теории упругости, применяемое для описания деформирования тонких стержней, балок, пластин. Рассмотрим задачу о расщеплении тонкой полосы сосредоточенными силами . Для применения критерия Гриффитса, нам надо знать выражение упругой энергии отщепляемой балки в зависимости от ее длины и нагрузок. В балочном приближении такая зависимость определяется.

Уравнение изгиба балки:

(8.1)

Здесь - момент инерции площади поперечного сечения балки относительно нейтральной оси, - перемещение балки, - распределенная нагрузка на балку. Для балок прямоугольного сечения толщиной и шириной :

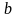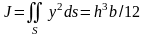
В сечении балки напряженное состояние характеризуется значением перерезывающей силы и моментом сил , которые через перемещение выражаются формулами: , .

Рассмотрим случай расщепления полосы сосредоточенными силами, приложенными на краю продольного разреза при . Граничные условия для определения перемещений в этой точке: , 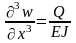. В конце разреза при принимаем выполнение условий жесткой заделки : .

Общее решение уравнения (8.1) при : 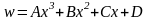Постоянные 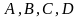можно найти из условия выполнения граничных условий

при : , , откуда следует

при : ,

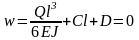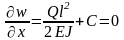
Из последнего уравнения следует и из предыдущего:

Таким образом, полностью определено перемещение отщепляемых полос. Найдем их упругую энергию, как работу по раздвижению точек приложения сил при их возрастании от 0 до : , где 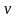- раскрытие разреза при : .

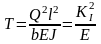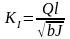В итоге . Известно, что плотность энергии, высвобождающейся при развитии разреза . Отсюда: и (8.2)

Учитывая, что для балки прямоугольного сечения 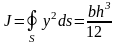, где - ширина балки, ее толщина, имеем:

При определении последней зависимости мы использовали критерий Гриффитса. Найдем локальный силовой критерий развития трещины при использовании балочного приближения. Для этого опишем деформирование расщепляемых полос у вершины разреза. Здесь имеем и , . Отсюда, сохраняя 3 члена ряда Тейлора, имеем: , где . Рассмотрим изменения, которые происходят с полосами при удлинении разреза на 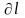. Перемещения в новом состоянии будут . Изменение перемещений вызовет изменение упругой энергии полос. Такое изменение можно рассчитать как работу момента и перерезывающей силы: . Знак – здесь из -за того, что работу совершают балки и их внутренняя энергия уменьшается.

Здесь

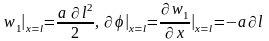
В итоге, сохраняя старший член по , получаем: и

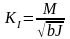. Полученное общее решение совпадает с найденным выше результатом (8.2) для частной задачи.