Билет 12

1. Комплексное представление напряжений и смещений Колосова-Мусхелешвили.

Рассмотрим случай плоской деформации и выразим функцию Эри через 2 аналитические функции. Так как функция Эри удовлетворяет бигармоническому уравнению, лапласиан от нее является гармоническим.

Обозначим гармоническую функцию 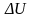через и сопряженную к ней через . Введем и рассмотрим первообразную этой функции

,

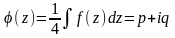Ее производная:

Отсюда

,

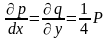Покажем, что функция 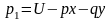гармоническая.

Найдем

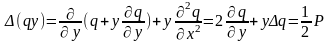
В итоге:

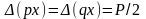, откуда

Отсюда , где .

Здесь

После преобразования получаем:

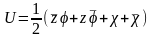. Отсюда:

И

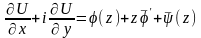(13)

Перейдем к представлению напряжений:

По формулам (6)

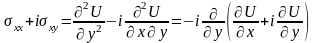
Используя (13), получим

,

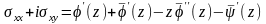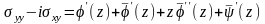
Складывая эти уравнения и вычитая первое из второго, получаем

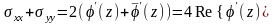(14)

или при переходе к сопряженным величинам имеем

(15)

Аналогично, используя закон Гука и интегрируя деформации, можно получить комплексное представление перемещений:

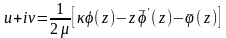(16)

для плоской деформации

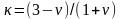для плоского напряженного состояния.

Эти представления были получены Г.В.Колосовым в 1909 г. и эффективно использованы Мусхелишвили, который развил методы теории функций комплексного переменного для решения широкого класса плоских задач теории упругости.

2. Расчет развития дисковой трещины при гидроразрыве.

Рассмотрим развитие дисковой трещины гидроразрыва. Примем во внимание, что продуктивный пласт, в котором развивается трещина, находится на большой глубине и сжат горным давлением . Развитие трещины происходит при закачке в нее с поверхности через скважину жидкости гидроразрыва, оказывающей давление на берега трещины . Будем считать жидкость идеальной и несжимаемой, а пласт непроницаемым для рабочей жидкости. Рассмотрим равновесное состояние дисковой трещины в таких условиях. Искомое поле напряжений можно представить как сумму поля сжатия горным давление упругого пространства без трещины и упругого пространства с трещиной, свободного от нагружения на бесконечности, но нагруженного на берегах трещины давлением . Легко видеть, что суммарное поле напряжений соответствует граничным условиям поставленной задачи. Раскрытие дисковой трещины под действием внутреннего давления и КИН известны:

, .

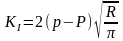Здесь 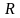- радиус дисковой трещины, модуль Юнга и коэффициент Пуассона упругой среды.

Раскрытая давлением дисковая трещина по форме является эллипсоидом. Объем его определяется через раскрытие в центре трещины и ее радиус по формуле:

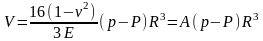. Отсюда , где .

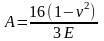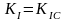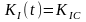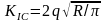В процессе гидроразрыва насосы поднимают давление в начальной трещине радиуса до момента, когда КИН трещины сравняется с критическим и трещина начнет развиваться. Найдем закон этого развития при условии медленного роста трещины и выполнения равенства . Из этого условия мы получаем связь давления с длиной трещины. Обозначим . Тогда и

.

В отсутствие утечек рабочей жидкости в пласт выполняется равенство объемов закаченной насосами жидкости и объема трещины :

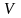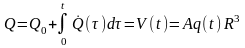, где - объем начальной трещины в момент страгивания.

Из приведенных соотношений, исключая давление получаем:

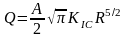и

Из этих формул видно, что при радиус трещины также стремится к бесконечности. При этом давление, раскрывающее трещину стремится к нулю.

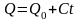Если насосы подают жидкость в трещину с постоянной скоростью , то . Здесь .

В этом случае трещина гидроразрыва развивается во времени по закону:

Оценим раскрытие трещины гидроразрыва радиуса 100м. Для горных пород примем: , , 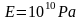. При таких значениях параметров: . . 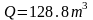Отсюда, раскрытие трещины в ее центре . Частицы проппанта, закачиваемого в трещину при гидроразрыве, должны быть меньше этого размера.

Оценим давление в трещине радиуса 100м

В начале развития трещины 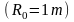потребуется избыточное давление 26.5 атм