Графики и ) Приближенные значения кин

Система бесконечного числа параллельных трещин в плоскости, растянутой по вертикали напряжением .

D

,

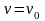
A

ё

B

C

При

При 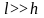исследуемую задачу можно приближенно свести к задаче о полубесконечной трещине в полосе (выделена на рисунке пунктиром), на краях которой касательные напряжения раны нулю и задано постоянное вертикальное смещение . КИН в такой задаче можно найти с помощью интеграла Райса.

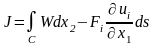, где контур С состоит из отрезков A, B, C, D

На горизонтальных отрезках контура интеграл равен 0, так как на них смещение постоянно и

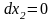
Интеграл на отрезке А равен нулю, так как там 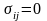(отрезок А находится далеко от кромки трещины и материал там разгружен разрезом)

Остается только интеграл по отрезку С. , Здесь . Для плоского напряженного состояния на отрезке С . Здесь учтено, что . В итоге и .

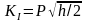Полученные предельные значения КИН при малых длинах трещин и больших определяют качественно зависимость КИН от длины трещины. С увеличением длины трещины КИН растет пропорционально корню из длины, затем этот рост замедляется и КИН асимптотически выходит на постоянное значение, пропорциональное корню из расстояния между трещинами.

Задача: Найти КИН системы параллельных длинных трещин при плоской деформации.

Трещина длиной находится в полосе шириной , растягиваемой напряжением Р

Границы полосы свободны от напряжений. Отсюда следует, что

и . Последнее равенство выполняется на вертикальных

прямых, симметрично разделяющих трещины в бесконечной

линейной цепочке, рассмотренной выше. Отличие состоит в том, что

в линейной цепочке полоса в районе трещины дополнительно

растянута по оси Х. Так как такое растяжение слабо сказывается

на Величине КИН, можно принять, что и здесь

. Лучшие результаты дает использование при формулы:

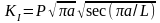
Аналогичные формулы для КИН можно применить для оценки напряженного состояния боковых трещин длиной , выходящих на свободные границы полосы . Для 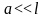известно: .

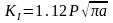Принцип суперпозиции для нахождения кин трещин.

Величина КИН трещин определяется как геометрией задачи, так и приложенной нагрузкой. Линейный характер теории упругости позволяет получать ее решение как сумму решений для задач с более простыми граничными условиями.

Как пример, найдем КИН прямолинейного разреза со свободными от нагрузок берегами в плоскости, нагруженной на бесконечности растягивающим напряжением . Решение задачи представим, как суперпозицию поля однородного растяжения плоскости и поля деформаций разреза, находящегося в свободной от напряжений на бесконечности плоскости, нагруженного изнутри давлением. Напряжения на месте разреза, расположенного вдоль оси Х в растянутой плоскости равны: , . Для того чтобы берега разреза были свободны, как это требует исходная задача, необходимо , чтобы второе поле скомпенсировало нагрузку берегов первого поля. Для этого надо, чтобы на берега разреза действовало давление . Тогда поле там будет: , .

Решение последней задачи нами определено ранее: . Так как поле равномерно растянутой плоскости не дает вклада в КИН, для КИН первоначально поставленной задачи о растяжении плоскости, содержащей свободный разрез имеем тоже выражение, что и для свободной плоскости с разрезом , нагруженным давлением изнутри. Более сложный пример дает рассмотрение задачи о растяжении полосы шириной с центральным разрезом длиной . 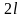К нижнему краю полосы приложена нагрузка . Эта нагрузка уравновешена силой, приложенной к верхнему берегу разреза: .

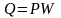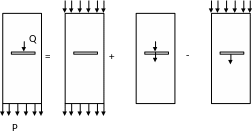
Искомое поле представляем как сумму трех полей, как показано на рисунке. Можно убедиться, что граничные условия поставленной задачи выполняются при сложении более простых задач и той же, поставленной. Имеем:

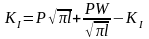. Отсюда