
- •Билет 1
- •Билет 2
- •Билет 3
- •Билет 4
- •Билет 5
- •Билет 6
- •Наклонная трещина в одноосном поле напряжений
- •Билет 7
- •Распределение напряжений вблизи вершины трещины
- •Билет 8
- •Антиплоская деформация
- •Билет 9
- •Билет 10
- •Критерий Райса
- •Билет 11
- •Подборка точных решений.
- •Взаимодействие трещин
- •Графики и ) Приближенные значения кин
- •Принцип суперпозиции для нахождения кин трещин.
- •Билет 12
- •Билет 13
Билет 1
Теоретическая прочность кристаллических тел на растяжение. Оценка теоретической прочности через модуль Юнга.
Рассмотрим идеальную атомную решетку бездефектного кристалла.
Для простоты рассуждений ограничимся рассмотрением кубической решетки с ребрами длиной а.

Атомы помещены в вершинах, узлах решетки. При деформации атомной решетки энергия связи меняется. Силы взаимодействия атомов определяются в основном зависимостью, описывающей изменение энергии взаимодействия U ближайших атомов при их отклонении от равновесного состояния. Кривую, качественно представляющую такую зависимость, можно построить, рассмотрев два соседних атома, причем один из них, например, левый, будем считать закрепленным (рис.1)

Рис. 1 Зависимость потенциальной энергии и напряжения от расстояния между соседними атомами.
Бесконечно удаленные атомы не взаимодействуют, а значит
 при
при

При сближении притягивающихся атомов их энергия взаимодействия убывает
Атомы нельзя совместить не разрушив их, поэтому при сближении атомов энергия взаимодействия неограниченно возрастает:
 при
при

Ближайший атом решетки находится на равновесном расстоянии
 ,
доставляющем минимум потенциальной
энергии взаимодействия:
,
доставляющем минимум потенциальной
энергии взаимодействия:

 при
при

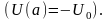
Отсюда
следует качественная зависимость
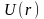 ,
изображенная на рис. 1 Сила взаимодействия
атомов
,
изображенная на рис. 1 Сила взаимодействия
атомов
 - это градиент потенциального поля
- это градиент потенциального поля
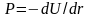 .
Если характерная площадь ячейки атомной
решетки
.
Если характерная площадь ячейки атомной
решетки
 ,
то можно ввести напряжения, определив
их следующим способом
,
то можно ввести напряжения, определив
их следующим способом
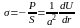 ,
,
Качественный
вид зависимости
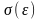 показан
на рис.1. Величину деформации решетки
при нагружении можно найти по формуле
показан
на рис.1. Величину деформации решетки
при нагружении можно найти по формуле
 .
В ненагруженном состоянии
и
.
В ненагруженном состоянии
и
 Интервал, на котором с ростом
Интервал, на котором с ростом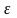 напряжения возрастают, описывает
диапазон устойчивого деформирования
решетки: рост деформации проводит к
увеличению напряжения. При разгрузке
решетка вернется в исходное равновесное
состояние.
напряжения возрастают, описывает
диапазон устойчивого деформирования
решетки: рост деформации проводит к
увеличению напряжения. При разгрузке
решетка вернется в исходное равновесное
состояние.
Интервал,
на котором с ростом
напряжения убывают, отвечает неустойчивому
состоянию решетки: деформация растет,
несмотря на падение напряжения. Эта
ветвь кривой показывает ослабление
взаимодействия атомов решетки при
разрыве атомной связи. Таким образом,
максимальное значение
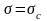 является пределом прочности межатомной
связи, называемым теоретической
прочностью. Оценим величину
является пределом прочности межатомной
связи, называемым теоретической
прочностью. Оценим величину
 .
Для твердых тел известны их сопротивляемость
слабому сжатию и растяжению, определяемую
модулем Юнга
.
Для твердых тел известны их сопротивляемость
слабому сжатию и растяжению, определяемую
модулем Юнга
 и предельная деформация при растяжении
и предельная деформация при растяжении
 Используем
эти величины для оценки
.
Аппроксимируем зависимость
функцией:
Используем
эти величины для оценки
.
Аппроксимируем зависимость
функцией:
 .
Максимум этой функции приходится на
относительную деформацию
.
Максимум этой функции приходится на
относительную деформацию
 (
( ),
что соответствует опытным данным.
),
что соответствует опытным данным.
Для
малых
определяем
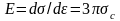 .
Отсюда
.
Отсюда
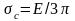
Решение задачи о прямолинейном разрезе, нагруженном изнутри постоянным давлением, вызывающем плоское деформирование отрыва (на основе комплексного представления Слепяна).
Трещины
отрыва,
раскрываемые давлением и расположенные
на прямой
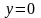 .
Этот случай отличается тем, что на оси
всей X
.
Этот случай отличается тем, что на оси
всей X
 .
Отсюда
.
Отсюда
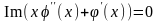 .
Это требование можно удовлетворить,
если принять, что выпоняется равенство
.
Это требование можно удовлетворить,
если принять, что выпоняется равенство
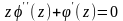 ,
откуда следует связь между
,
откуда следует связь между
 и
и :
:
 .
Подставляя это выражение в (15) и заменяя
на
.
Подставляя это выражение в (15) и заменяя
на
 ,
получим:
,
получим:
 ,
откуда:
,
откуда:
Из
(14) следует
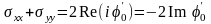 .
Решая систему уравнение для
.
Решая систему уравнение для
 и
и ,
получаем:
,
получаем:
 ,
,
 ,
,
 (17)
(17)
Найдем
выражения для смещений через
 :
:
Из
(16) следует:
 .
.
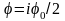
Отсюда:

Или

Отсюда смещения выражаются формулами:
 ,
,
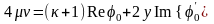 (18)
(18)
В
задаче о прямолинейной трещине,
расположенной на оси X
в интервале
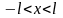 и нагруженной изнутри давлением
,
имеем следующие граничные условия для
аналитической функции
и нагруженной изнутри давлением
,
имеем следующие граничные условия для
аналитической функции
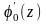 :
при
:
при
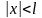
 ,
,
при
 ,
так как
,
так как
 ,
,
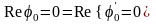 .
.
Эти граничные условия совпадают с условиями аналогичной задачи в антиплоской постановке теории упругости.
