52

Механика трещин

НГУ- 2009г.

Лекции 1-2. Введение. Физические основы прочности и разрушения твердых тел. Критерий хрупкого разрушения Гриффитса.

Механика трещин или механика хрупкого разрушения является составной частью механики разрушения твердых тел. Последняя включает в себя тот раздел науки о сопротивлении материалов, который изучает заключительные стадии процесса деформирования. Исследования по вопросам прочности были начаты еще Леонардо да Винчи и Галилеем, установившим, что разрушающая нагрузка пропорциональна площади сечения растягиваемого бруса и не зависит от его длины. В дальнейшем трудами Кулона, Сен-Венана, Мора были положены начала теории предельного равновесия. Согласно этим теориям в результате различных испытаний материала, таких как одноосное растяжение стержней, изгиб балок, растяжение тонкостенных трубок с приложенным внутренним давлением и др. определяются в пространстве напряжений области, в которых материал выдерживает нагрузки без разрушения (рис.1).

Рис.1 Пример паспорта прочности для горных пород . Сплошная линия и пунктир – разные аппроксимации опытных данных

При этом не учитывается возможное присутствие дефектов типа пор или трещин, которые могут вызвать хрупкое разрушение при сравнительно низком уровне напряжений.

Гриффитс в 1920 г опубликовал первую работу по теории хрупкого разрушения - разрушения, вызванного развитием трещин. Эта теория получила быстрое развитие в связи с участившимися случаями внезапного разрушения крупных конструкций, которые стали применяться в промышленности, за счет развития магистральных трещин. Это, например, корпуса кораблей, газопроводы, корпуса ракет. Так в 1946 г было зафиксировано 132 случая разрушения корпусов кораблей, а к концу 1958 г. - уже 319 ( Г. Либовиц). Все эти катастрофы были связаны с внезапным развитием трещин. Необходимо было понять явление и найти способы борьбы с ним.

С другой стороны изучение механики трещин актуально для повышения эффективности технологических процессов разрушения твердых сред, широко применяемых в горном деле. Здесь следует отметить разрушение горных пород при взрыве, ударе и гидроразрыве.

Взрывной способ разрушения горных пород в настоящее время является основным при добыче твердых полезных ископаемых. Понимание процессов развития трещин особенно важно в следующих взрывных технологиях,

1. Хрупкое разрушение в дальней зоне взрыва радиальными трещинами. Их развитие, густота, размер

2. Камуфлетное взрывание. Снижение напряжения. Повышение фильтрации при выщелачивании.

3. Контурное взрывание. Создание щелей - волновых экранов

У дарное разрушение горных пород применяется при работе многих машин ударного действия, как ручных (отбойные молотки), так и навесных - молота экскаваторов с ковшом активного действия. Для прочных, хрупких горных пород здесь важно оценить размеры откалываемых кусков в зависимости от свойств пород и параметров удара, в первую очередь энергии (рис.2).

Рис.2 Схемы работы ударных инструментов

Непосредственное применение теория хрупкого разрушения имеет для развития технологий гидроразрыва горных пород, применяющихся для интенсификации добычи нефти (рис.3) и для направленного разрушения горных пород.

Рис.3 Схема образования вертикальной трещины при гидроразрыве нефтяного пласта

Теория хрупкого разрушения позволяет решать задачи о равновесии и развитии трещин при деформировании твердых тел.

Обычно развитие трещины начинается с начальной зародышевой трещины. Это может быть дефект изготовления материала, например, при сварке корпуса корабля, или микродефект, возникающий спонтанно в результате тепловой флуктуации в твердом теле при нагрузке или внедрении чужеродных атомов. Такие неоднородности появляются уже на кристаллическом, атомарном уровне.

Рассмотрим вопросы прочности на простейших кристаллических моделях твердого тела.

1.Физические основы прочности и разрушения твердых тел.

1. Теоретическая прочность материалов

2. Экспериментальные данные

3. Масштабный фактор

4. Практические способы повышения прочности

5. Общая характеристика структурных уровней дефектов в материалах. Модель сплошной среды

В естественном (не деформированном) состоянии твердого тела все атомы кристаллической решетки находятся в условиях равновесного взаимодействия, имеющего электромагнитную и квантовую природу. На долю заряженных частиц (ядер и электронов приходится приблизительно 10^-15 объема, занимаемого телом. Остальной объем – это вакуум, пронизанный электромагнитными полями взаимодействия. О характере сил, обеспечивающих неизменность формы твердого тела, можно судить по такому сопоставлению. Порядок среднего межатомного расстояния a=10^-10м, а средний радиус атомного ядра r₀=10^-15м. Сравнивая отношение a/r₀ c отношением расстояния от Земли до Солнца к радиусу Земли, получим, что эти отношения одного порядка: a/r₀=10⁵, L/R=2,3*10⁴. Таким образом, взаимодействие сил на микроуровне сопоставимо с дальнодействием гравитационного поля на планетарном уровне. Для твердых тел различного химического состава энергия связи в равновесном состоянии неодинакова. Различают связи в молекулярных, ионных, ковалентных кристаллах и металлах. У некоторых соединения, например у графита, связи могут быть смешанными.

К молекулярным кристаллам относятся почти все органические кристаллы с внутренними вандервальсовыми связями между молекулами (парафин). Энергия таких связей меняется в диапазоне 10-50 кДж/моль.

Ионная связь ( в неорганических кристаллах типа NaCl, LiF и др.), определяется кулоновским взаимодействием ионов ( )и имеет большую энергию связи 500-800 кДж/моль(одновалентная) и 1000-1800 кДж/моль (двухвалентная).

Самая прочная – ковалентная связь (алмаз, германий, кремний), ее энергия 800-1400 кДж/моль. Химическая связь нейтральных атомов имеет квантовую природу. Атомы как бы объединяют свои оболочки. К таким веществам относятся полупроводники.

У металлов валентные электроны становятся общими и стягивают положительные ионы атомов, уравновешивая их отталкивание. Энергия связи металлов равна 130-500 кДж/моль.

1. Теоретическая прочность материалов

Рассмотрим идеальную атомную решетку бездефектного кристалла.

Для простоты рассуждений ограничимся рассмотрением кубической решетки с ребрами длиной а.

Атомы помещены в вершинах, узлах решетки. При деформации атомной решетки энергия связи меняется. Силы взаимодействия атомов определяются в основном зависимостью, описывающей изменение энергии взаимодействия U ближайших атомов при их отклонении от равновесного состояния. Кривую, качественно представляющую такую зависимость, можно построить, рассмотрев два соседних атома, причем один из них, например, левый, будем считать закрепленным (рис.1)

Рис. 1 Зависимость потенциальной энергии и напряжения от расстояния между соседними атомами.

1. Бесконечно удаленные атомы не взаимодействуют, а значит при

2. При сближении притягивающихся атомов их энергия взаимодействия убывает

3. Атомы нельзя совместить не разрушив их, поэтому при сближении атомов энергия взаимодействия неограниченно возрастает: при

4. Ближайший атом решетки находится на равновесном расстоянии , доставляющем минимум потенциальной энергии взаимодействия: при

Отсюда следует качественная зависимость , изображенная на рис. 1 Сила взаимодействия атомов - это градиент потенциального поля . Если характерная площадь ячейки атомной решетки , то можно ввести напряжения, определив их следующим способом

,

Качественный вид зависимости показан на рис.1. Величину деформации решетки при нагружении можно найти по формуле . В ненагруженном состоянии и Интервал, на котором с ростом напряжения возрастают, описывает диапазон устойчивого деформирования решетки: рост деформации проводит к увеличению напряжения. При разгрузке решетка вернется в исходное равновесное состояние.

Интервал, на котором с ростом напряжения убывают, отвечает неустойчивому состоянию решетки: деформация растет, несмотря на падение напряжения. Эта ветвь кривой показывает ослабление взаимодействия атомов решетки при разрыве атомной связи. Таким образом, максимальное значение является пределом прочности межатомной связи, называемым теоретической прочностью. Оценим величину . Для твердых тел известны их сопротивляемость слабому сжатию и растяжению, определяемую модулем Юнга и предельная деформация при растяжении Используем эти величины для оценки . Аппроксимируем зависимость функцией: . Максимум этой функции приходится на относительную деформацию ( ), что соответствует опытным данным.

Для малых определяем . Отсюда

Рассмотрим для примера кристалл NaCl. Молекулярный вес молекулы 59. Это означает, что 59 г NaCl содержит 6*10²³ (число Авогадро) молекул и 12*10²³ атомов. Отсюда в 1г вещества содержится 2*10²² ионов Na и Cl. Если учесть, что плотность кристаллического NaCl примерно 2г/см³, то

Экспериментальные данные по деформированию кристаллов NaCl дают оценку , отсюда

Полученная выше оценка максимально допустимого напряжения отличается от реально наблюдаемого в экспериментах значения прочности на растяжение в 100- 1000 раз. Например, для монокристалла каменной соли NaCl указанные значения отличаются в 600 раз: =3000Мпа, =5Мпа.

Оценка теоретической прочности при сдвиге. Сдвиг- это скольжение одной атомной плоскости по другой, при котором все атомы одной плоскости сдвигаются относительно другой на одно и тоже расстояние .

Здесь

Потенциальная энергия решетки при сдвиге является периодической функцией деформации с периодом 1. Она минимальна в положении равновесия, когда и максимальна в промежуточном состоянии, т.е. при Минимумам и максимумам соответствуют устойчивые и неустойчивые положения равновесия решетки. Если , то после снятия напряжений решетка вернется в исходное состояние (упругая деформация). Если то произойдет самопроизвольный переход в ближайшее положение устойчивого равновесия , т.е. деформация станет пластической ( скольжение атомных слоев может продолжится с последующей деформацией ,если внешнее напряжение не снято).

Я.И.Френкель(1926 г.) предложил аппроксимировать зависимостью

Напряжение сдвига определяется по производной от потенциальной энергии по

Отсюда следует, что напряжение будет максимально тогда, когда . Такое напряжение примем за теоретический предел прочности при сдвиге . При малых напряжение сдвига и угол сдвига связаны законом Гука . ( - модуль сдвига), а так как при деформация приближенно равна углу сдвига, имеем связь с .

,

из которой следует оценка теоретической прочности при сдвиге: .

Для меди значение на три порядка больше , определяемой экспериментально: , .

2. Эксперименты по обнаружению теоретической прочности.

В удивительном по простоте опыте по подтверждению теоретической прочности, проведенном А.Ф.Иоффе (1924) поверхностный слой монокристалла NaCl смывался водой после чего кристалл испытывался на разрыв. При этом была получена прочность - сопоставимая со значением теоретической прочности . Прочность необработанных водой образцов равна 5Мпа. Этот эксперимент подтверждает гипотезу о превалирующей роли поверхностных микротрещин в понижении прочности образца. Объемные дефекты внутри монокристалла, конечно, так же влияют на прочность (1600, а не 3000 МПа), но, как оказалось, меньше, чем поверхностные.

Предположение о кардинальном влиянии дефектов основано на следующем интуитивно очевидном рассуждении. Разрушить бездефектный кристаллический образец можно, разорвав одновременно (или практически одновременно) все связи между двумя параллельными атомными плоскостями. Дефектность приводит к тому, что разрыв связей в сечении происходит не одновременно, а последовательно в вершине трещины, прорастающей из дефекта.

В последнем случае разрушающее внешнее усилие, затрачиваемое на последовательное разрушение ближайших к вершине трещины связей, будет существенно меньше, чем то, которое необходимо для одновременного разрыва всех межатомных связей в сечении. Против гипотезы о понижении прочности материала начальными микротрещинами, распределенными в сплошном теле, имеются доводы. Один из них основан на оценках, которые показывают, что дефекты в стали, способные понижать ее прочность до реально наблюдаемого значения, должны быть столь велики, что их можно легко обнаружить. Это несоответствие теоретически предсказанных размеров дефектов с наблюдаемыми объясняется, возможно, неучетом поликристалличности и, соответственно, существования множественных межзеренных дефектов. Известно, охрупчивание металлов связано с присутствием в них горофильных (любящих границу) примесей, главные из которых являются фосфор и сурьма. При охлаждении расплпва стали и его кристаллизации такие примеси вытесняются (диффундируют) на границы формирующихся зерен. Содержание примесей на границах становится в 100 и более раз выше, чем в объеме зерен. Связь зерен при этом оказывается менее прочной и поэтому, поликристалические тела разрушаются, как правило, по границам зерен. Повышая прочность стали, обычно стараются уменьшить количественное содержание таких вредных примесей или делают добавку вязкого молибдена, затрудняющего их диффузию при кристализации. Тем не менее, даже малые количества горофильных примесей могут, вероятно, существенно понизить прочность сплавов. Это подтверждается новыми техническими решениями получения сверхпрочных металлов. Так один из разработанных способов получения таких сталей основан на более равномерном распределении примесей в аморфном состоянии металла. При чрезвычайно быстром охлаждении (на 10⁶ градуса в секунду) вязкого расплава, состоящего на 80% из металла и на 20% из вязких металлоидов, атомы не успевают выстроится в решетку и расплав застывает не кристаллизуясь, сохраняя хаотическое расположение, свойственное жидкостям, стеклам. Технологически это осуществляется путем охлаждения струйки металла на вращающемся со скоростью 1000 об/мин массивном барабане. Расплав вытягивается в ленту металлического стекла толщиной в несколько десятков микрон, шириной в несколько сантиметров и длиной в десятки метров. Прочность такой ленты всего в 4 раза меньше теоретической прочности металла .

Аморфное состояние металла не является устойчивым и при нагреве его свыше 100^о со временем происходит кристаллизация, протекающая тем быстрее, чем больше температура.

2. Масштабный фактор.

В 1920 г. А.А. Гриффитс провел серию экспериментов по разрушению стеклянных образцов. Одна из серий была связана с испытаниями на разрыв тонких цилиндрических стеклянных нитей. Установлено, что прочность нитей монотонно увеличивается с уменьшением их диаметра (табл.1)

Таблица 1

d мкм	2.5	8	12.5	16	22
	5500	2000	1400	1000	220

( )

Гриффитс предположил, что прочность нитей понижается с увеличением толщины из-за дефектов, которые существуют в материале в виде мельчайших микротрещин. Чем меньше диаметр нити, тем меньше вероятность образования опасных микротрещин в испытуемой нити и тем она прочнее. Аналогичный опыт с известково-натриевыми стеклянными стержнями выполнен в 30-х годах Андеренгом. Растяжению подвергались стержни примерно равного диаметра, но разной длины. Получены следующие данные (табл. 2).

Таблица 2

	5	10	20	45	90	183	1560
	13.0	13.5	12.5	13.0	12.7	12.7	13.0
	15	12.2	12.1	11.5	7.6	8.7	7.2

Результаты экспериментов определенно показывают на то, что увеличение длины стержня, а значит рост вероятности существования опасных дефектов, при неизменном диаметре, приводит к уменьшению прочности. В частности, отсюда можно заключить, что прочность больших тел меньше, чем малых, так как их дефектность больше.

Обнаружение начальных микротрещин в стекле оптическими методами затруднительно. Дело в том, что по оценкам дефекты, влияющие на прочность, имеют линейный размер и оптически прозрачны, так как практически не имеют толщины. Для выявления начальных дефектов в стекле был разработан специальный, не разрушающий образцы метод ионного обмена. Известково-натриевое стекло погружается в ванну с расплавом лития и азотнокислого калия, который добавлен в расплав для снижения температуры плавления. Ионы натрия в стекле способны к обмену, в данном случае они заменяются в приповерхностном слое меньшими ионами лития. Такая замена в решетке приводит к усадке материала в поверхностной пленке толщиной и соответственно к растяжению вдоль поверхности, а значит и к раскрытию имевшихся там дефектов. Специальными методами тонирования на площадке в 1 см² обнаружено несколько десятков тысяч дефектов. После обработки поверхности стекла плавиковой кислотой дефекты почти полностью исчезали.

2. Повышение прочности материалов и создание новых материалов повышенной прочности.

Эксперимент Иоффе указывает на один из способов повышения прочности материалов, который заключается в удалении поверхностных микротрещин. Путем механического упрочнения поверхностного слоя, а также травлением и очисткой поверхности от трещин, создаются, например, высокопрочные стекла. При этом их прочность меняется следующим образом.

1. Необработанные массивные изделия из стекла (оконные стекла, емкости) обладают самой низкой прочностью .

2. Химическое или физическое упрочнение поверхности стекла позволяет повысить прочность до значений .

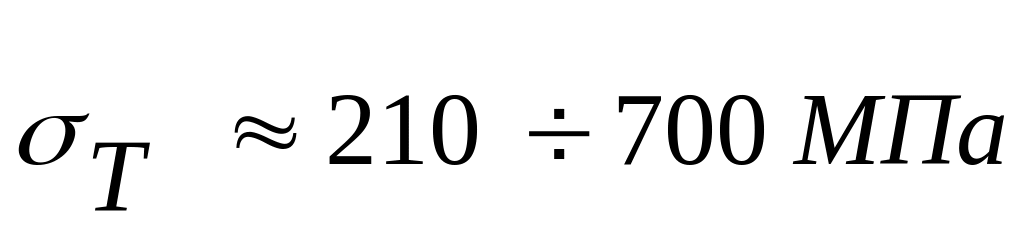3. Стекловолокна и стекла, травленные плавиковой кислотой, имеют прочность .

4. Сверхпрочность достигается в специальных условиях. Так в опытах Журкова, проведенных в 30-34 годах, разрушение плавленого кварца в вакууме происходило при .

Аналогичные величины прочности были получены Морли при разрыве стеклянных образцов в жидком азоте.

Существенное повышение прочности стеклянных нитей, как отмечено выше, связано не только с очисткой поверхности, но и с масштабным эффектом. Именно масштабный эффект повышения прочности лежит в основе создания новых современных материалов - композитов. Из тонких сверхпрочных нитей изготавливают основу, которую заливают или запекают в менее прочный материал. Назначение основы - нести основную нагрузку, а заполнитель, фиксируя прочные, но гибкие волокна, препятствует изменению формы изделия, которое может произойти из-за смещения нитей относительно друг друга. Наибольшее распространение получили композиты из стеклянных нитей в эпоксидной смоле - стеклопластики. Характеристики стеклопластика: , , , определяют как его основное достоинство - высокую прочность на единицу веса (в 4 раза выше, чем у стали), так и недостаток - из-за малости модуля Юнга возникают большие деформации. Поэтому в конструкциях стеклопластики трудно сочетать с другими материалами, которые, как правило, деформируются меньше. Известны другие композиты, которые изготавливают используя высокую прочность нитей. Свойства некоторых приведены в табл. 3.

Таблица 3.

Вид волокна	стеклянные	органические	борные	угольные
	2400	2800	3500	1500-3000

Достаточно длинные волокна получают вытяжкой из расплавов или напылением на тончайшие нити. Для сравнения приведем значения прочности распространенных конструкционных материалов.

Материал	сталь	титан	алюминий
	1500	1000	500

5. Общая характеристика дефектов в материалах. Сплошная среда.

Итак, любое твердое тело ослаблено большим количеством дефектов и несовершенств атомной решетки. Как это влияет на процессы деформирования и как это учитывать при построении расчетных моделей? Разрушение - это процесс их роста и слияния в нагружаемом твердом теле, который в итоге приводит к частичному или полному изменению формы тела, разделению его на части (фрагментация).

Взаимодействие дефектов зависит от их числа, плотности распределения и относительных размеров. Можно принять такую условную градацию масштабов нарушений в твердом теле.

1. Несовершенства типа точечных дефектов кристаллической решетки и дислокаций, а также нарушений в виде микродефектов, возникающих при взаимодействии дислокаций ( ). Обычно распределение их является равномерным и изотропным.

Среди дефектов кристаллической решетки , как сказано выше, выделяют термодинамически равновесные (точечные) дефекты и дислокации - линейные дефекты кристаллической решетки, нарушающие правильное чередование атомных плоскостей. К дефектам первого типа относятся:

• Вакансия - отсутствие атома в каком - либо узле решетки.

• Подмена атома решетки "чужим" атомом.

• Межузельный атом.

Все они возникают из-за тепловых флуктуаций и нарушают ближний порядок. Дефекты второго типа - дислокации нарушают дальний порядок.

Различают два типа дислокаций: краевую и винтовую. Ориентацию дефектности решетки задает вектор Бюргерса (указан стрелкой на рис.6) Обычной мерой дефектности служит плотность дислокаций - количество дислокационных линий, пересекающих единичную площадку. В реальных кристаллах до нагружения на площадке 1см² насчитывается до 10⁶ линий дислокаций - из 100 атомных связей одна нарушена. Под нагрузкой к моменту выхода на пластический режим деформирования плотность дислокаций увеличивается до 10¹⁴/см². Одиночной дислокации энергетически не выгодно находится внутри тела, поэтому даже при небольших нагрузках она стремится выйти на границу или слится с дислокацией противоположного знака. Коллективное поведение дислокаций иное. При высокой плотности взаимодействие дислокаций препятствует их свободному перемещению в теле. Более того, в некоторых местах дислокации скапливаются либо, стопоря друг друга, либо сгущаясь возле включений или границ зерен. В этих случаях происходит объединение сотен и более дислокаций одного знака- возникают микротрещины.

2. Дефекты в виде микротрещин, межзеренных нарушений или линий скольжения, локализованных в плоскостях ( ).

С развитием дефектов на данном уровне становится более существенным влияние нарушенности микроструктуры на макропараметры сплошной среды, в частности, на прочность. Начиная с некоторого момента исчезает изотропия пространственного распределения дефектов - это сказывается на поведении нагружаемого материала: возникает неупругость, либо образуются протяженные микротрещины.

2. Макротрещины ( ) - наиболее длинные трещины, размер которых сравним с размерами рассматриваемого тела или его конструктивного элемента. Именно развитие макротрещин приводит к полному разрушению тела ( разделению на несколько частей). Очевидно, зарождение, размеры и поведение макротрещин под действием нагрузок связаны с теми первоначальными изменениями, которые происходят на различного масштаба микроуровнях. Примером учета процессов изменения структуры дефектности на микроуровнях и итоговой процесса разрушения является теория временной прочности Журкова. По Журкову в нагруженном твердом теле в результате термических флуктуаций постоянно происходит появления дефектов его структуры, например, смещения атома в решетке с образованием дыры и лишнего атома в междоузлии. Скорость появления дефектов определяется уровнем напряжения и температурой тела.

,

где -плотность дефектов, напряжение, температура. Анализ результатов экспериментов показал, что при достижении плотности дефектов критической величины происходит ускорение процессов их слияние и роста размеров, последовательный переход дефектов на новый масштабный уровень и, наконец, к образованию макроскопических трещин. Отсюда для времени нахождения твердого тела, первоначально свободного от дефектов, под постоянной нагрузки имеем соотношение:

При выводе соотношений механики деформирования сплошной среды обычно отказываются от рассмотрения индивидуальных взаимодействий элементов структура (в том числе микродефектов и микротрещин), заменяя среду некой обобщенной, в которой структура строения среды игнорируется, а учитываются лишь интегральные (осредненные) характеристики. При таком подходе получается континуальная модель реальной среды - картина микромира наблюдаемая на макроуровне. Равномерность распределения микродефектов внутри микрообъемов, достаточно представительных на микроуровне, но малых сравнительно с объемом всего тела, делают такое осреднение по множеству всех микрообъемов устойчивым. Под точкой сплошной среды (частицей), получаемой в результате такого осреднения, в механике понимается минимальный объем дискретной среды, способный передать основные черты и свойства, присущие материалу в большом объеме.

Широко распространенная для описания деформаций твердого тела линейная теория упругости следует из равномерности распределения в теле большого числа микродефектов, а также из неизменности осредненных характеристик от микродефектов, когда внешняя нагрузка меняется в некотором диапазоне. Все это обеспечивает линейную связь напряжений и деформаций, наблюдаемую экспериментально. Ускоренное развитие и объединение микродефектов, микротрещин, которое имеет место, начиная с некоторого уровня внешней нагрузки, находит отражение в выполаживании зависимости напряжения от деформации - наступает пластичность. Если объединение и рост дефектов происходит весьма быстро, то диаграмма обрывается практически на упругой стадии. Такие материалы, разрушение которых происходит при незначительной пластичности называются квазихрупкими, а само разрушение - хрупким. Именно этот тип разрушения, для которого применимы соотношения линейной теории упругости, будет в основном рассмотрен в этом в данном курсе.

Рассматривая поведение тела с трещинами, будем считать, что трещина - это разрез вдоль некоторой поверхности внутри тела, не имеющий толщины и что поверхность трещины является частью общей поверхности, ограничивающей объем, занимаемый сплошным телом.

Если при этом деформирование тела с неразвивающейся трещиной описывается в рамках теории упругости, то рост трещины определяется не только процессами, происходящими на макроуровне с учетом влияния изменяющихся геометрии тела и условий нагружения, но и процессами, которые происходят на различного масштаба микроуровнях вблизи вершины трещины- в точке с позиции механики сплошной среды. Разрушение в микрообъеме, соответствующем этой точке, и, в частности, для бездефектной структуры определяется только взаимодействием атомов в решетке. В общем случае, ставя условия, позволяющие описать разрушение тела с трещиной, приходится так или иначе учитывать процесс разрушения этого характерного микрообъема - учитывать структуру материала и его нарушений на разных уровнях микроструктуры. Общепринятый подход, применяемый при изучении хрупкого разрушения, заключается в решении задачи о напряженном состоянии тела с трещиной методами механики сплошной среды. Условие разрушения тела в вершине трещины вводится отдельно. Оно, как правило, связывает характеристики напряженного состояния в вершине трещины с параметрами материала, определяющими его трещиностойкость.

Теория хрупкого разрушения Гриффитса.

Гриффитс в своих работах объяснил расхождение теоретических оценок прочности кристаллических тел с найденными экспериментально значениями влиянием микротрещин. При этом он указал, как рассчитать предельное состояние тела с трещинами под нагрузкой. Он использовал энергетический подход и постулировал, что на образование новых поверхностей за счет роста трещины необходимы затраты энергии. При увеличении на площади трещины дополнительная работа внешних сил идет на увеличение упругой энергии тела и поверхностной берегов трещин:

, .

Если при виртуальном увеличении трещины высвобождающейся энергии хватает на затраты по образованию новой площади, то трещина будет развиваться, в противоположном случае роста трещины не будет. Такое условие равновесия трещины Гриффитс в случае плоского деформирования сформулировал в виде неравенства

,

где - длина трещины

Пусть внешние силы, действующие на тело, занимающее область , - вектор перемещений точек тела,

Энергию , высвобождающуюся при единичном приращении длины трещины, можно записать в виде:

(1)

Если при виртуальном увеличении трещины , то трещина будет развиваться. В противоположном случае роста трещины не будет.

Высвобождение энергии при росте трещины можно увидеть на простом примере. Рассмотрим растянутую полосу с закрепленными в дальнейшем краями. Если ее медленно разрезать в поперечном направлении, то запасенная в полосе энергия будет исчезать, силы, действующие на зажимы, уменьшатся. Так как тело упругое, то высвобождающая энергия может поглощаться только в вершине трещины, где и происходит разрыв материала.

Рассмотрим два способа вычисления

Пусть внешние силы расположены вне некоторой окрестности у вершины трещины. В положении равновесия наложим на тело жесткие связи там, где приложены внешние силы. Тогда при единичном удлинении трещины выделится энергия

, (2)

Где символом обозначена производная упругой энергии при замороженных связях, когда внешние силы не работают.

Пусть теперь связи на силы не накладываются. Тогда для фиксированной трещины при ее нагружении в силу линейности задачи имеем:

,

где поле перемещений зависит от длины трещины . Докажем это. Перейдем от ненагруженного состояния к нагруженному линейно по времени. Пусть в каждой точке, где приложены силы ( ), Тогда, в силу линейности: . Работа, совершенная внешними силами, перейдет в упругую энергию:

Предположим, что силы не меняются при удлинении трещины (мягкое нагружение). Тогда

Возвращаясь к выражению (1) для , получим:

(3)

Покажем, что правые части формул (2) и (3) равны друг другу. Начальные состояния до вариации трещин в рассматриваемых случаях одинаковы. Состояние после вариации длины трещины во втором случае можно получить из первого, заменив связи их реакциями и увеличив затем последние до первоначальных значений внешних сил. При этом работа внешних сил и упругая энергия деформации получат одно и тоже приращение. И, следовательно, высвободившаяся энергия (2) не изменится. Таким образом, высвобождающаяся энергия равна уменьшению упругой энергии деформации тела в условиях, когда при вариации длины трещины внешние силы не работают, или увеличению упругой энергии (равной половине работы внешних сил) в условиях, когда при той же вариации на тело не накладывается никаких дополнительных связей.

В своей статье Гриффитс рассмотрел прямолинейную трещину длиной 2l , находящуюся в бесконечной плоскости, растягиваемой внешним напряжением в перпендикулярном к плоскости трещины направлении.

При расчетах Гриффитс воспользовался решением задачи о растянутой плоскости с эллиптическим вырезом. Мы воспользуемся решением задачи о равновесии разреза длиной 2l в плоскости, растянутой напряжением P. Согласно этому решению известна форма берегов разреза:

. (4)

Используя это выражение можно найти величину высвободившейся энергии растянутой пластины при появлении в ней трещины. Рассмотрим последовательно переход из напряженного состояния растянутой плоскости без разреза к плоскости с разрезом. Введем согласно рис.2 состояния 0-3.

Рис. 2. Последовательные состояния растянутой плоскости при раскрытии в ней трещины.

Переход из состояния 0 в 1 не меняет энергию упругой плоскости. При переходе из 1 в 2 такое изменение происходит. Для расчета изменения надо перейти от 1 к свободному от нагрузок разрезу (состояние 2) постепенно уменьшая растягивающее напряжение, приложенное к его берегам от значения P до 0 . Графики раскрытия разреза в разных его точках от напряжения P приведены на рис.3. При этом будет совершена работа, определяемая площадью под этим кривыми

Рис.3 Уменьшение напряжения на берега разреза при его раскрытии до состояния свободной от напряжения трещины в разных ее точках

(5)

Получаем, что уменьшение упругой энергии при переходе из состояния 1 в 2 равно . Отсюда и из (2) следует

Заметим здесь, что переход из состояния (2) в (3) (рис.2), которое можно совершить заменяя связи силами и затем увеличивая их до положенного значения, не приводит к выделению энергии, так как вся работа переходит в упругую энергию.

В рассматриваемом случае условие равновесного состояния трещины является: , так как трещина удлиняется симметрично вправо и влево по оси .

Учитывая это из (6) следует:

- критическая нагрузка, превышение которой приводит к неограниченному росту трещины.

Из приведенной для критической нагрузки формулы следует:

(3)

Это соотношение Гриффитс проверял экспериментально, разрушая внутренним давлением стеклянные полые шары и трубки. Предварительно в стекле создавались трещины разной длины. В эксперименте фиксировалось давление, при котором происходило разрушение. Результаты приведены для шаров в таблице 1

2l, inch	D, inch	P, lbs.per sq/inch
0.15	1.49	864	237
0.27	1.53	623	228
0.54	1.60	482	251
0.89	2	366	244

Экспериментально для исследуемого стекла Гриффтс определил значение поверхностной энергии, как 0.0031 lbs. per inch =0.0031*4.45N/0.025=0.55Н/m. Это значение было получено экстраполяцией данных о поверхностной энергии жидкого стекла при снижении температуры расплава. Расчет по формуле (3) для значений параметров стекла дает =266. Это замечательное согласие с экспериментом.

В последствии многими экспериментами была подтверждена теория Гриффитса, были разработаны методики определения для конструкционных материалов, и для многих материалов она была найдена. Это позволяет расчетами определять уровень безопасных нагрузок в конструкциях, содержащих трещины. Для проведения таких расчетов надо уметь находить напряженное состояние упругих тел под нагрузкой при наличии в них трещин.

Рассмотрим постановки задач теории упругости для тел с трещинами.

Задача: Для шара и цилиндра найти напряжения растяжения их стенок, если задано: диаметр, толщина стенок, внутреннее давление.