Вопрос 14

Операторы цикла while и repeat. Оператор цикла предназначен для многократного выполнения заданной последовательности операторов.  К таким операторам относятся:  - оператор цикла с предусловием (while)  - оператор цикла с постусловием (repeat)  - оператор цикла с параметром (for)  Оператор цикла с предусловием  while <выражение булевского типа> do <оператор>;

Порядок выполнения: - вычисляется значение <выражения булевского типа>, стоящего после while; - если true, тогда выполняется оператор после do, после чего осуществляется переход к началу цикла; - повторяется до тех пор, пока значение не станет false, после этого осуществляется выход из оператора. Совокупность многократного выполнения операторов обычно называется телом цикла.

Пример. eps:=0.001; while x > eps do x:=x/2;

ВОПРОС 15 Метод дихотомии есть метод половинного деления. Пример-задачка, дабы мне проще было это объяснить. Ваш друг задумал целое число от одного до десяти включительно. Он честно отвечает на ваши вопросы «да» или «нет». Какое минимальное число вопросов вам потребуется, чтобы гарантированно отгадать задуманное число?

Под фразой «гарантированно отгадать» следует понимать, что какое бы число из диапазона   ни было загадано, задавая вопросы в соответствии с некоторым правилом, вам заведомо хватит   вопросов, где   — искомый минимум. Строго говоря, предлагается не только ответить на вопрос задачи, но и составить алгоритм отгадывания задуманного числа за минимальное число вопросов. В данном случае в ответ закрадываются степени двойки. Для того, чтобы передать один из двух возможных вариантов, требуется один бит. Два бита могут передать один из   вариантов. Три бита — один из   вариантов. С помощью   бит можно передать один из  вариантов. В какую минимальную степень   необходимо возвести двойку, чтобы она стала больше десяти? В четвёртую,  . Из предыдущего абзаца следует, что четырёх вопросов будет достаточно для отгадывания. Первая часть задачи решена.

А как следует задавать вопросы, чтобы уложиться в дозволенные четыре вопроса? Уж точно не отгадывать число по порядку, начиная с единицы — это ведёт в худшем случае к девяти вопросам. Общее правило одно — нужно каждым вопросом уменьшать неопределённость в два раза. Если число вариантов не является степенью двойки, то в некоторых вопросах количество вариантов в «половинах» может различаться, но не более, чем на единицу. Итак, перед первым вопросом мы имеем десять различных вариантов. Десять пополам — пять. Спросим: «Задуманное число больше пяти?» Теперь самое главное не ошибиться нигде на единицу, не сказать не подумав «больше» вместо «больше либо равно» и наоборот.

После ответа на первый вопрос вариантов осталось пять. Нам нужно разбить их на группы, состоящие из двух и трёх элементов. Например, если выяснилось, что задуманное число больше пяти, корректно будет спросить: «Верно ли, что задуманное число больше либо равно восьми?»

Третьим вопросом мы снижаем число вариантов с двух до одного, либо с трёх до двух. Если после второго вопроса осталось всего два варианта (например, на вопрос: «Число больше либо равно восьми?» последовал отрицательный ответ), то потребуется всего три, а не четыре вопроса. В любом случае, последним вопросом мы выбираем между двумя оставшимися числами и узнаём ответ.

Описанный метод называется методом деления пополам или, по-научному, дихотомией.

ВОПРОС 16 Метод бисекции или метод деления отрезка пополам — простейший численный метод для решения нелинейных уравнений вида f(x)=0. Предполагается только непрерывность функции f(x). Поиск основывается на теореме о промежуточных значениях Алгоритм основан на следующем следствии из теоремы Больцано — Коши:

Пусть непрерывная функция  , тогда, если  , то  .

Таким образом, если мы ищем ноль, то на концах отрезка функция должна быть противоположных знаков. Разделим отрезок пополам и возьмём ту из половинок, на концах которой функция по-прежнему принимает значения противоположных знаков. Если значение функции в серединной точке оказалось искомым нулём, то процесс завершается.

Точность вычислений задаётся одним из двух способов:

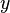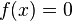1.  по оси  , что ближе к условию   из описания алгоритма; или

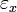2. , по оси  , что может оказаться удобным в некоторых случаях.

Процедуру следует продолжать до достижения заданной точности.

Для поиска произвольного значения достаточно вычесть из значения функции искомое значение и искать ноль получившейся функции. Псевдокод Пусть

• x_n – начало отрезка по х;

• x_k – конец отрезка по х;

• x_i – середина отрезка по х;

• eps_y – требуемая точность вычислений по y (заданное приближение |F(x_i)| к нулю).

Тогда алгоритм метода бисекции можно записать в псевдокоде следующим образом:

1. Начало.

2. Ввод x_n, x_k, eps_y.

3. Если F(x_n) = 0, то Вывод (корень уравнения – x_n).

4. Если F(x_k) = 0, то Вывод (корень уравнения – x_k).

5. Пока |F(x_i)| > eps_y повторять:

6. dx := (x_k + x_n) / 2;

7. x_i := x_n + dx;

8. если sign(F(x_n)) ≠ sign(F(x_i)), то x_k := x_i;

9. иначе x_n := x_i.

10. конец повторять

11. Вывод (Найден корень уравнения – x_i с точностью по y - eps_y).

12. Конец.