25. "Вечная" рента. Рента пренумерандо. Отложенные ренты.

Вечная рента. под вечной рентой понимается ряд платежей, количество которых не ограничено – теоретически она выплачивается в течение бесконечного числа лет.

Современная величина вечной ренты есть конечная величина, которая определяется весьма просто. при  пределом для коэффициента приведения является .a Откуда для вечной ренты находим A=R/i. Рента пренумерандо. отличие этой ренты от постнумерандо в том ,что каждый платеж делается на 1 интервал раньше. Современная стоимость и наращенная сумма такой ренты находятся по формуле A=(1+i)*R*a(n,i), S=(1+i)*R*s(n,i). Отложенные ренты. Начало выплат у отложенной ренты сдвинуто вперед относительно некоторого момента времени. Пусть рента выплачивается спустя t лет после некоторого начального момента времени, обозначим современную стоимость через 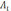.Пусть современная стоимость немедленной ренты равна А. Тогда .равна величине A,дисконтированной за t лет.A =A*v’=R*a(n,i)* v’.

26. Потребительский кредит и его погашение. Льготные кредиты.

Потребительский кредит. При выдаче потребительского кредита сразу на всю сумму кредита начисляются простые % ,они прибавляются к величине самого кредита и сумма всех погашающих выплат должна быть равна этой величине.Существует несколько схем погашения потребительского кредита:погашение равными срочными уплатами. Пусть кредит D взят на n лет при годовой ставке простых % i Тогда общая сумма выплат составит D*(1+ni).Если в году предусмотрено m выплат,то имеем одну выплату,равную Y=D*(1+n*i)/m*n. процентные деньги при этом рассчитываются по «правилу»78. Погашение основного долга равными выплатами . При этом способе основной долг D выплачивается равными долями P=D/nm,а процентные деньги –выплатами,уменьшающимися в арифметической прогрессии,и последняя выплата равна разности этой прогрессии . Такай способ определения процентных выплат называют правилом 78. Льготные кредиты. Льготные кредиты выдают по льготной ставке меньшей обычной ставке. Фактический заемщик получает субсидию равную разнице соотв.современных сумм. Пусть кредит размером Д выдан на n лет ,по льготной ставке д меньшей обычной ставке i и будет погашен равными выплатами величиной R.Эти выплаты образуют годовую ренту с современной величиной. Разность Z-R есть ежегодные потери кредитора. Наращенная сумма субсидии наз-ся общими потерями кредитора.

27.Понятие ренты. Классификация рент.

Специальный поток платежей ,в котором переменные интервалы между двумя последовательными положительными платежами постоянны, называется финансовой рентой. Финансовая рента возникает, например, при выплате %по облигациям либо при погашении потребительского кредита. Рента характеризуется следующими параметрами:

1)член ренты-размер отдельного платежа

2)период ренты-временной интервал между двумя платежами

3)срок ренты-время от начала первого периода до конца последнего

4)% ставка

Классификация рент:

1)по количеству выплат в течение года ренты делятся на:

а)дискретные

-годовые(1 раз в год)

-р-срочные(р раз в год)

б)непрерывные

2)по числу раз начислений % в течение года ренты делятся на ренты:

-с ежегодным начислением %

-с начислением % m раз в году

-с непрерывным начислением %

3)по величине членов ренты

-постоянные

-переменные

4)по вероятности выплат

-верные(выплачиваются в обязательном порядке)

-условные(выплачиваются в зависимости о наступления определенного события)

5)по количеству членов

-ограниченные

-бесконечные

6)по срокам выплат

-немедленные

-отложенные

7)по моменту выплат платежей в пределах периода ренты

-обыкновенные(постнумерандо)когда платеж осуществляется в конце периода.

-пренумерандо, когда платеж осуществляется в начале периода.