42. Поток платежей и его доходность. Понятие мгновенной доходности.

Поток платежей (англ. cash flow) — это последовательность денежных сумм, каждая из которых отнесена к некоторому моменту времени (такие денежные суммы называются «датированными»).

Пусть {Rk,tk} – поток платежей, в нем tk – моменты времени, Rk – платежи. Будем говорить, что рассматриваемый поток имеет современную величину А при уровне доходности j, если ∑Rk/(1+j)tk=А. Если поток есть годовая рента с годовым платежом Rи длительностью n, то рента имеет современную величину А при уровне доходности j, если R*а(п,])=А. Фиксируем А, тогда при увеличении Rдоходность ренты увеличивается. Можно сказать и по–другому: для увеличения доходности ренты надо увеличить годовой платеж.

Все эти соображения особенно хорошо видны на примере вечной ренты, поскольку для нее А=R/j, или, по-другому: доходность вечной ренты есть j=R/А. Важно отметить, что определенная таким образом доходность потока платежей не зависит от ставки процента, а зависит только от величины и моментов самих платежей, в силу чего ее называют часто внутренней доходностью потока платежей.

Более точно внутренняя доходность потока платежей есть такая его доходность в только что определенном смысле, при которой современная величина этого потока равна нулю (такая характеристика имеется не у всякого потока платежей).

Понятие мгновенной доходности.

Пусть в момент tкапитал равен К(t),а через небольшое время ∆tкапитал равен K(t+∆t), тогда средняя доходность dна отрезке

[t,t+ t]

в процентах годовых (в долях) равна K(t+ t)/K(t)=(1+

при малом

величина (1+d)

с точностью до бесконечно малых 2-го порядка равна 1+d*

Устремляя получаем

Итак, мгновенная доходность есть производная по времени натурального логарифма капитала или, как говорят, логарифмическая производная. В частности, при постоянной мгновенной доходности dкапитала растет во времени по экспоненте:

K(t)=K(0)*

43. Погашение традиционной ипотечной ссуды.

Погашение традиционной ипотечной ссуды (ТИС)

Такая ссуда выдается на 10-30 лет под небольшие проценты. Обычно ее выдают под залог имущества (земли, дома и т.д.). В случае невозврата ссуды в установленный срок заложенное имущество становится собствен­ностью кредитора. ТИС погашается равными ежемесячными выплатами, проценты также начисляются ежемесячно.

Пусть номинальный размер ссуды равен D и она выдана на срок n лет под годовую ставку сложных процентов i. Равные ежемесячные вы­платы равны

Традиционно определяют на конец любого года и остаток, который еще предстоит выплатить. Пусть r_k - остаток на конец к -го года. Он вы­числяется как разность между наращенной величиной выданной ссуды и наращенной величиной ренты выплат:

R*

44. Переменные расходы по займу. Формирование погасительного фонда.

Пусть ряд срочных уплат представляет собой геометрическую прогрессию со знаменателем q, тогда этот ряд можно записать в виде членов переменной ренты Y, Yq, Yq2,...,Yqn-1. Приравняв современную стоимость этой ренты сумме первоначального долга, находим:

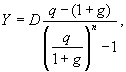
где q - заданный годовой темп роста платежей, g - процентная ставка по займу.

Далее находятся срочные уплаты и разрабатывается детальный план погашения. В ряде случаев размеры срочной уплаты связываются с ожидаемыми поступлениями средств и задаются заранее в виде графика погашения. Размер последней срочной уплаты не задается. Она определяется как сумма остатка долга на начало последнего периода.

Формирование погасительного фонда.

Для погашения задолженности может быть создан специальный по­гасительный фонд, в котором будут накапливаться средства, чтобы пога­нь займ одним платежом в конце срока. Ясно, что это имеет смысл лишь [тогда, когда на деньги погасительного фонда начисляются более высокие проценты, чем те, под которые взят займ.

К концу срока займ составит D* (1 + i и ежегодный платеж должен cоставлять

R=