32. Непрерывные случайные величины.

СВ наз. величины к-рые могут принимать те или иные значения заранее до опыта неизвестно какие именно. Различают дискретные и непрерывные СВ.

Дискретные СВ.

Значения обознач х₁,х₂,…,х_n,…

Всякое описание значений, к-рые может принимать СВ и соответствующие этим значениям вероятности наз. законом распределения СВ.

Для дискретной СВ:

xi	X1	X2	…	xn
pi	P1	P2	…	pn

;

Если функция распределения непрерывной случайной величины дифференцируема, то более наглядное представление о случайной величине дает плотность вероятности случайной величины px (x), которая связана с функцией распределения Fx (x) формулами

и 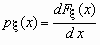. Отсюда, в частности, следует, что для любой случайной величины .

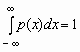33. Математическое ожидание.

Если случ величина Х задана законом распределения, то M(X)= при условии что ряд сходится. Мат ожидание назыв средним значением, а также центорм распределения. Для мат ожидания употребл и другие обозначен ЕХ,m,a. Мат ожидание непрерывн случайной величины Х, все значения которой принадлежат отрезку [a,β], определяется формулой. M(X)= ю мат ожидания случ величины обладает след свойствами: мат ожидания случайной величины заключено между ее наименьшим и наибольшим значениями. Мат ожидания постоянно равно этой постоянно М(С)=С.постоянный множитель можно выносить за знак мат ожидания М(СХ)=СМ(Х)

34. Дисперсия и её свойства.

Дисперсия дискретнслучайн вел-ны-мат ожидание квадрата отклонения случайн вел-ны от ее мат ожидания.Теорема:Дисперсия равна разности между мат ожиданием квадрата случайной вел-ны Х и квадратом ее мат ожидания.Св-ва дисперсии:1)Дисперсия постоян вел-ны равна нулю.2)Постоян множитель можно выносить за знак дисперсии, возводя его в квадрат.3)Дисперсия суммы двух независслучайн вел-н равна сумме дисперсий этих вел-н. 4)Дисперсия разности двух независслучайнвел-н равна сумме дисперсий этих величин.Теорема:Дисперсия числа появления  события А в п независимых испытаний, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании.Фор-ла:

35. Начальные и центральные моменты. Мода и медиана.

Модой М_о (Х) непрерывной случайной величины Х называют то ее возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет 2 одинаковых максимума, то его называют бимодальным.

Медианой М_е(Х) непрерывной случайной величины Х называют то ее возможное значение, которое определяется равенством: Р[Х<М_е(Х)]=Р[Х>М_е(Х)].

Геометрически медиану можно истолковать как точку, в которой ордината f(х) делит пополам площадь, ограниченную кривой распределения.

Начальный теоретический момент порядкаk непрерывной случайной величины Х определяется равенством

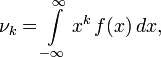
Центральный теоретический момент порядкаk непрерывной случайной величины Х определяется равенством [х-М(Х)]^кf(х)dх.

Центральные моменты выражаются через начальные моменты по формулам: