27. Действия с вероятностями. Условная вероятность.

Условная вероятность — вероятность одного события при условии, что другое событие уже произошло.

Пусть   — фиксированное вероятностное пространство. Пусть   суть два случайных события, причём  . Тогда условной вероятностью события   при условии события   называется

.

Действия с вероятностями: Сложение вероятностей. Условная вероятность, умножение вероятностей. Формула полных вероятностей и формула Байеса. Аксиоматика А.Н. Колмогорова при построении общей вероятностной модели. Примеры непрерывных вероятностных пространств. Геометрические вероятности.

28. Формула полной вероятности.

Пусть имеется группа событий B₁,B₂,..., B_n, обладающая следую­щими свойствами:

1) все события попарно несовместны

2) их объединение образует пространство элементарных исходов

В этом случае будем говорить, что B₁, B₂,...,B_n образуют полную группу событий. Такие события иногда называют гипотезами.

формула полной вероятности:P(A)=P(B1)*P(A/B1)+ P(B2)*P(A/B2)+ P(Bn)*P(A/Bn)

29. Формула Бернули.

где

Это ур-ние имеет вид: (7). Это ур-ние сводится к лин. уравнению (7а). Сделаем замену переменной: (8), . Подставляем это в (7а), получаем: - получение лин. уравнения, кот можно решать, например, методом вариации постоянной.

30. Дискретные случайные величины.

Перемен.величина x,кот принимается в результате испытаний между конечной и бесконечной последовательности значений x1,x2,…,хn,…наз . дискретной случайной величиной. отношение, устанавливающее связь между отдельными возможными значениями случайной величины и соответств. им вероятностями, наз. законом распред. дискретн. случайной величины. Дискрет.случайная величина мот быть задана различн.способами

1)табличн

Значение х х1 х2 … хn Вероятность р Р1 Р2 … рn 2)графический

3)аналитический

Pk=(xk)Т.к случайная величина принимает одно из своих возм значений, то .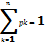

Значение величины имеющая наиб вероятность называется модой

31. Функция распределения.

Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия. ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ —вероятность того, что случайная величина X примет значение, меньшее, чем х, где х — произвольное действительное число:F(x) = Р{Х ≤ х} =   F(x) — неубывающая функция; О ≤ F(x) ≤ 1. Ф. р. в. полностью задает случайную величину. Если X —дискретная случайная величина, принимающая значения х₁, x₂... с вероятностями p₁,p₂,..., то ее функция распределения будет:F(x) = ∑р_k; она разрывна и возрастает скачками в точках х_k. Если X — непрерывная случайная величина, то у нее существуетплатность распределения вероятностей f(x) и Ф. р. в. будет: .Примерами дискретных Ф. р. в. являются биноминальная, распределение Пуассона; непрерывных Ф. р. в, — нормальное, равномерное распределение. Важнейшими характеристиками Ф. р. в. являются моменты. В геол. и геохим. исследованиях выяснение истинных Ф. р. в. представляет сложнейшую и важнейшую задачу, с решением которой связано большинство практических и теоретических проблем.