24. Аксиоматическое определение вероятности.

Пусть  - произвольное пространство элементарных событий, а   - такая совокупность случайных событий, для которой справедливо:   , AB , A+B    и A\B , если A  и B   .

Числовая функция P, определенная на совокупности событий  , называется вероятностью,если:

P(A)  0 для любого A из  ;

P( ) = 1;

если A  и B    несовместны, то P(A+B) = P(A) + P(B);

для любой убывающей последовательности событий {A_i}из  , , такой, что 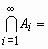  , имеет место равенство  .

Тройку   называют вероятностным пространством.

25. Формула классической вероятности.

Классическая формула для определения вероятности наступления случайного события X выглядит следующим образом: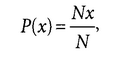 

где Nx — количество вариантов возможного наступления случайного события х;

N— общее количество возможных исходов. Пример. Бросая игральную кость, мы можем получить шесть возможных исходов — выпадение одной из шести граней игральной кости: 1,2,3, 4, 5 или 6. Таким образом, можно определить вероятность выпадения одной из граней, например 3: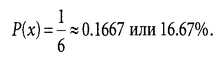 

Таким образом, вероятность выпадения одной из граней игральной кости (в нашем примере 3) составляет 16.67%.

Можно также определить вероятность выпадения одной из двух граней (например, 2 или 3). В этом случае используется правило сложения вероятностей, а вероятность рассчитывается следующим образом:

Р(х8; By) = Р{х) + Р{у) = 0.1667 + 0.1667 = 0.3333 или 33.33%,

где Р(х) — вероятность наступления случайного события х (в нашем примере 2);

Р(у) — вероятность наступления случайного события у (3).

Таким образом, вероятность выпадения грани с цифрой 2 или 3 равна 33.33%.

Правило сложения вероятностей используется для зависимых событий, когда одно случайное событие исключает наступление другого случайного события.

Если необходимо найти вероятность одновременного наступления двух и более случайных событий, используется правило умножения вероятностей. При этом все события должны быть независимы друг от друга.

Пример. В результате одновременного броска двух игральных костей мы можем получить 36 различных комбинаций: 1 — 1,1—2,1—3,1—4,1— 5, 1—6, 2—1, 2—2, 2—3 и т.д. Для определения вероятности того, что в результате подбрасывания мы получим на гранях обеих игральных костей по 1, используем правило умножения вероятностей:

Р(х8; 87) = Р{х)хР{у) = 0.1667x0.1667 = 0.0278 или 2.78%

Таким образом, вероятность одновременного выпадения на двух игральных костях граней с цифрой 1 равна 2.78%.

26. Геометрическая вероятность .

Геометрическая вероятность — один из способов задания вероятности; пусть Ω — ограниченное множество евклидова пространства, имеющее объем λ(Ω) (соответственно длину или площадь в одномерной или двумерной ситуации), пусть ω — точка, взятая случайным образом из Ω, пусть вероятность, что точка будет взята из подмножества   пропорциональна его объёму λ(x), тогда геометрическая вероятность подмножества  определяется как отношение объёмов:

Аналогично определяется геометр. вероят-ность события, когда множ-во Ω представ-ляет собой нек. область на плоскости или отрезок на прямой линии. В этих случаях объемы областей заменяются, соответст-но, площадями фигур или длинами отрезков.

Случайное событие – событие, которое может произойти (не произойти), если будет выполнена определённая совок-сть условий S, которая наз. испытанием.

Несколько событий наз совместными, если в результате испытания появление 1-го из них не исключает появления другого в одном и том же испытании.

Несколько событий наз несовместными, если в результате испытания появ-ление 1-го из них исключает появление других (остальных) событий в одном и том же испытании (выпадение очков на игральной кости – 6 несовмес. событий).

2 события наз. равновозможными, если нет оснований считать, что появление одного из них более возможно, чем появление другого. (выбрасывание орла и решки - равновозможные события).

Полная группа событий – совок-сть случаных событий, если в результате испытания появится хотя бы 1 из них.

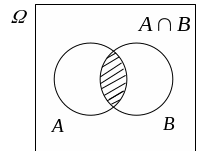
С= или – сумма событий А и В (событие, которое заключается в том, что происходит либо событие А, либо событие В, либо события и А и В).

или – произведение собы-тий (событие, которое состоит в том, что одновременно происходят события А и В).

- противоположное событию А (если эти события несовместны, а их сумма – достоверное событие)-(Промах или попадание про стрельбе по мишени)