22. Вычисление тройного интеграла.

1. Предположим, что функция f(x, y, z) непрерывна в рассматриваемой области T.Пусть сначала T = [a, b; c, d; e, f] - прямоугольный параллелепипед, проектирующийся на плоскость yz в прямоугольник R = [c, d; e, f]. Тогда

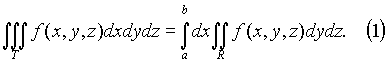Заменяя в (1) двойной интеграл повторным, получим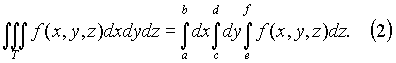

Вычисление тройного интеграла сводится к последовательному вычислению трёх определённых интегралов.Если первые два интеграла в (2) объединить в двойной, то будем иметь

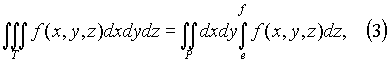где P = [a, b; c, d] - проекция параллелепипеда T на плоскость xy.Заметим, что в этих случаях можно менять роли переменных.2. Пусть область T заключена между плоскостями x = a и x = b, причём каждое сечение области T плоскостью  представляет собой квадрируемую фигуру G(x)(рис. 1). Тогда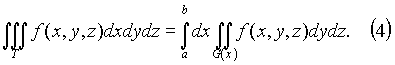

3. Пусть теперь тело T представляет собой "цилиндрический брус", ограниченный снизу и сверху, соответственно, поверхностями z = z₁(x, y) и z = z₂(x, y), проектирующиеся на плоскость xy в некоторую квадрируемую фигуру G (рис.2), z₁(x, y) и z₂(x, y) - непрерывны в G. Тогда

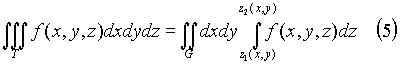Если G = {(x, y): a  x  b, y1(x)  y  y2(x)}, то

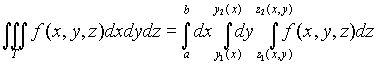Отметим, что наряду с указанными формулами имеют место и им подобные, получающиеся перестановкой переменных x, y и z.

23. Пространство элементарных событий. Алгебра событий.

Каждый из равновозможных результатов испытаний называется элементарным исходом или (элементарным событием). Всякий мыслимый результат эксперимента называют элементарным событием и обычно обозначают буквами 

Пространством элементарных событий называется множество всех взаимно исключающих исходов эксперимента такое, что результатом эксперимента всегда является один и только один исход.

Пространство элементарных событий обычно обозначается   и считается заданным, если указаны все его элементы.Из элементарных исходов можно составить более сложное событие. Результат испытания называется событием, независимо от его значимости. Результат испытания, который нельзя заранее прогнозировать, называется случайным событием.

Любое подмножество данного множества   интерпретируется как событие (возможно, и ненаблюдаемое). Совокупность всех наблюдаемых событий составляет множество событий для данного эксперимента.

Множество   для данного испытания может быть дискретным, или иметь более сложную структуру. К дискретным относятся конечные или счетные множества элементарных исходов. Построение множества  (если оно не задано при описании эксперимента) осуществляется на практике, исходя из требования, чтобы все интересующие нас результаты данного эксперимента могли быть однозначно описаны на основе построенного множества  .Другими словами, если нас интересуют события   и т.д., являющиеся наблюдаемыми событиями в данном эксперименте, то множество   должно состоять из таких исходов, чтобы существовали подмножества данного множества, равносильные событиям   и т.д.

Наступление события, благоприятствующие исходы

Каждое случайное событие А определяется как подмножество в множестве элементарных событий  . При этом те элементарные события из  , при которых событие А наступает (т.е. принадлежит подмножеству А) называют благоприятствующими событию А. Говорят, что событие А произошло (наступило, осуществилось, реализовалось), если результатом эксперимента явился элементарный исход  , принадлежащий А ( ).

Совместные (совместимые), несовместные (несовместимые) события

Два события называются совместными (совместимыми) в данном опыте, если появление одного из них не исключает появления другого.

Два события называются несовместными (несовместимыми) в данном опыте, если они не могут произойти вместе при одном и том же испытании. Несколько событий называются несовместными, если они попарно несовместны.

Другими словами, события А и В совместны, если соответствующие множества А и В имеют общие элементы, и несовместны в противном случае, если появление одного из них исключает появление другого, и соответствующие множества А и В не имеют общих элементов, т.е. пересечение этих множеств является пустым множеством.