16. Вычисление двойного интеграла по области криволинейной трапеции.

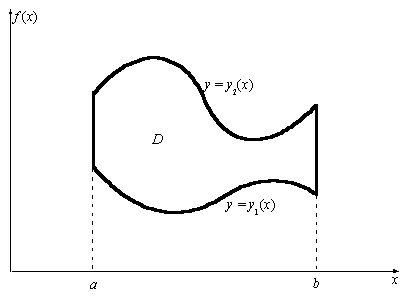
Рис. Область интегрирования в виде криволинейной трапеции

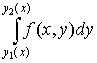Теорема. Если существует и существует , то существует 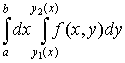и имеет место равенство .

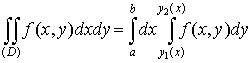17. Криволинейные координаты на плосоксти.

18. Площадь плоской фигуры в криволинейных координатах.

f(x) 0, = площади криволинейной трапеции:

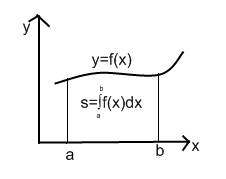
Пусть требуется найти S области огранич.

слева и справа отрез.прямых x=a,x=b, снизу

граф.функции y=f₁(x) и сверху y=f₂(x), f₂(x) f₁(x)

Эта S равна разности

площадей и графиками ф-ций y=f₁(x), y=f₂(x),т.е.разность

соотв. опред. интегралов.

S= или

S= f₁(x)]dx.

19. Формула Грина.

Пусть в плоскости Oxy задана область R, ограниченная замкнутой, кусочно-непрерывной и гладкой кривой C. Предположим, что в некоторой области, содержащей R, задана непрерывная векторная функция

с непрерывными частными производными первого порядка 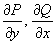 . Тогда справедлива формула Грина

где символ   указывает, что кривая (контур) C является замкнутой, и обход при интегрировании вдоль этой кривой производится против часовой стрелки.  Если  , то формула Грина принимает вид

где S − это площадь области R, ограниченной контуром C.  Формулу Грина можно записать также в векторной форме. Для этого введем понятия ротора векторного поля.  Пусть векторное поле описывается функцией

Ротором или вихрем векторного поля   называется вектор, обозначаемый   или   и равный

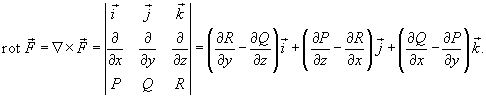
Формула Грина в векторной форме записывается в виде

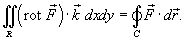
20. Приложения двойных интегралов.

1.   Вычисление площадей

2.   Вычисление объёмов тел

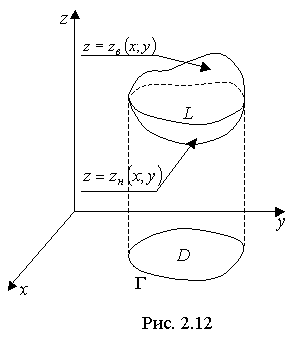
Пусть тело V ограничено (рис. 2.12)сверху — только одной поверхностью  z = z_в(x; y); снизу — только одной поверхностью z = z_н(x; y). Линия Lпересечения этих поверхностей проектируется в границу Г области D, на которой заданы непрерывные функции  z = z_в(x; y), z = z_н(x; y).

При этих условиях:

Доказательство формулы (2.17) легко провести на основе геометрического смысла двойного интеграла.

3.   Центр тяжести плоской фигуры

Если 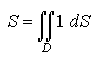    ,   то координаты х_c и у_c центра С находятся так:

21. Тройной интеграл. Необходимое и достаточное условие существования.

Тройной интеграл. Необходимое и достаточное условие существования.

Рассмотрим замкнутую пространственную область (V) и функ­цию f(x,у,z), определенную в этой области. Область (V) разобьем произвольным способом на n элементарных областей (∆V₁), (∆V₂), …(∆V_n) диаметрамиd₁d₂..., d_n и объемами ∆V₁, ∆V₂, ..., ∆V_n Наибольший из диаметров обозначим буквойd. В каждой элементарной области(∆Vk) выберем произвольно одну точку Mk(Xk, Уk, Zk) и составим произведение f(xk, уk, zk) ∆Vk.

Интегральной суммой для функцииf(x, у,z) по области (V)

называется сумма вида   ∑f(xk, yk,zk)∆Vk.

Тройным интегралом от функцииf(x, у,z) по области (V) на­зывается конечный предел интегральной суммы при d→0:

∫∫∫f(x, у,z)dV=lim∑f(x_k,у_k, z_k) ∆V_k.

Если функцияf(x, y, z) непрерывна в области (V), то указан­ный предел существует и конечен (он не зависит от способа раз­биения области (V)на элементарные области и выбора точекМk).

Основные свойства тройных интегралов аналогичны свойствам двойных интегралов.

В прямоугольных декартовых координатах тройной интеграл обычно записывают в виде: ∫∫∫f(x, y, z) dxdydz.