
- •1.Числ.Ряды.Необх.Признак сход-и.
- •3.Признак Даламбера.
- •4. Радикальный признак Коши.
- •5. Интегральный признак Коши.
- •6.Теор Признак Лейбница
- •7. Теор Признак Вейерштрасса о равномерной сх-ти.
- •8. Степенные ряды. Теорема Абеля.
- •13. Приложения криволинейных интегралов.
- •14. Двойной интеграл.Необходимое и достаточное условие существования двойного интеграла.
- •16. Вычисление двойного интеграла по области криволинейной трапеции.
- •17. Криволинейные координаты на плосоксти.
- •18. Площадь плоской фигуры в криволинейных координатах.
- •19. Формула Грина.
- •20. Приложения двойных интегралов.
- •21. Тройной интеграл. Необходимое и достаточное условие существования.
- •22. Вычисление тройного интеграла.
- •23. Пространство элементарных событий. Алгебра событий.
- •24. Аксиоматическое определение вероятности.
- •25. Формула классической вероятности.
- •27. Действия с вероятностями. Условная вероятность.
- •28. Формула полной вероятности.
- •29. Формула Бернули.
- •30. Дискретные случайные величины.
- •31. Функция распределения.
- •32. Непрерывные случайные величины.
- •33. Математическое ожидание.
- •34. Дисперсия и её свойства.
- •35. Начальные и центральные моменты. Мода и медиана.
- •36. Нормальный закон.
- •37. Производящие функции.
- •38. Характеристические функции.
- •39. Дискретные двумерные случайные величины.
- •40. Непрерывные двумерные случайные величины.
- •41. Функции от случайных величин.
- •42. Неравенство Чебышева.
- •43. Теорема Чебышева.
- •44. Центральная предельная теорема.
- •45. Теорема Бернулли.
- •46 Выборка. Эмпирическая функция, полигон частот, гистограмма.
- •48. Точечные оценки. Метод моментов.
- •49. Метод максимального правдоподобия.
- •50. Интервальная оценка для математического ожидания случайной величины, распределенной по нормальному закону.
48. Точечные оценки. Метод моментов.
ТОЧЕЧНАЯ ОЦЕНКА
-
статистическая оценка, значения к-рой
суть точки во множестве значений
оцениваемой величины.
Пусть
по реализации ![]() случайного
вектора
случайного
вектора ![]() принимающего
значения в выборочном пространстве
принимающего
значения в выборочном пространстве ![]()
![]() надлежит
оценить неизвестный параметр
надлежит
оценить неизвестный параметр ![]() (или
нек-рую функцию
(или
нек-рую функцию ![]() Тогда
любая статистика Т n=Т п (Х),осуществляющая
отображение множества
Тогда
любая статистика Т n=Т п (Х),осуществляющая
отображение множества ![]() в
в ![]() (или
в множество значений функции
(или
в множество значений функции ![]() наз.
точечной оценкой параметра
наз.
точечной оценкой параметра ![]() (оцениваемой
функции
(оцениваемой
функции ![]() Важными
характеристиками Т. о. Т п являются
ее математич. ожидание
Важными
характеристиками Т. о. Т п являются
ее математич. ожидание
![]() и
дисперсионная матрица (ковариационная
матрица)
и
дисперсионная матрица (ковариационная
матрица)
![]()
Вектор ![]() наз.
вектором ошибок Т. о. Т п.
Если
наз.
вектором ошибок Т. о. Т п.
Если
![]() -
нулевой вектор при всех
-
нулевой вектор при всех ![]() то
говорят, что Т п является
несмещенной оценкой функции
то
говорят, что Т п является
несмещенной оценкой функции![]() или
что Т п лишена
систематич. ошибки, в противном случае
Т. о. Т п наз.
смещенной, а вектор
или
что Т п лишена
систематич. ошибки, в противном случае
Т. о. Т п наз.
смещенной, а вектор ![]() -
смещением или систематической ошибкой
Т. <о. Качество Т. о. определяется с
помощью функции риска.
-
смещением или систематической ошибкой
Т. <о. Качество Т. о. определяется с
помощью функции риска.
Метод моментов
Вместе
с тем, на основе наблюдений ![]() могут
быть найдены выборочные начальные
моменты
могут
быть найдены выборочные начальные
моменты ![]() -го
порядка
-го
порядка
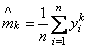 ,
,
которые
служат состоятельными оценками моментов
распределения ![]() .
.
Метод моментов
заключается в приравнивании ![]() выборочных
моментов к соответствующим моментам
распределения и нахождении оценок
неизвестных параметров из системы
уравнений:
выборочных
моментов к соответствующим моментам
распределения и нахождении оценок
неизвестных параметров из системы
уравнений:
![]() .
.
Кроме начальных моментов, для оценок параметров могут использоваться центральные моменты распределения и выборочные центральные моменты:
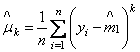 .
.
Для некоторых
распределений, например, нормального
или экспоненциального, оценки параметров,
найденные с помощью метода моментов,
совпадают с соответствующими ОМП.
Вместе с тем имеются многочисленные
задачи, в которых метод моментов приводит
к худшим по точности оценкам, чем метод
максимального правдоподобия. Характерным
примером является оценка
параметра ![]() равномерного
распределения
равномерного
распределения ![]() .
Для нахождения этой оценки на основе
метода моментов приравняем математическое
ожидание (первый начальный момент)
.
Для нахождения этой оценки на основе
метода моментов приравняем математическое
ожидание (первый начальный момент) ![]() и
выборочное среднее
и
выборочное среднее 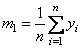 .
В результате получаем несмещенную
оценку
.
В результате получаем несмещенную
оценку ![]() с
дисперсией
с
дисперсией 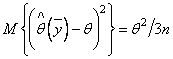 .
Заметим, что найденное значение в
.
Заметим, что найденное значение в ![]() раз
больше дисперсии (2.27) оценки максимального
правдоподобия. Приведенный результат
подчеркивает целесообразность поиска
эффективных оценок с помощью метода
максимального правдоподобия. Однако
встречаются примеры, где решение
уравнений правдоподобия найти не
удается, но можно получить хорошие
оценки по методу моментов. Рассмотрим
два таких примера.
раз
больше дисперсии (2.27) оценки максимального
правдоподобия. Приведенный результат
подчеркивает целесообразность поиска
эффективных оценок с помощью метода
максимального правдоподобия. Однако
встречаются примеры, где решение
уравнений правдоподобия найти не
удается, но можно получить хорошие
оценки по методу моментов. Рассмотрим
два таких примера.
Пусть требуется
оценить параметры ![]() и
и ![]() гамма-распределения
(табл. 1.1). Приравнивая моменты
распределения
гамма-распределения
(табл. 1.1). Приравнивая моменты
распределения ![]() и
и ![]() к первому
к первому ![]() и
второму
и
второму ![]() выборочным
моментам, получаем следующие оценки
параметров по методу моментов:
выборочным
моментам, получаем следующие оценки
параметров по методу моментов:
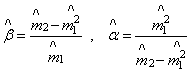 .
.
Проанализируем
теперь возможности решения более сложной
задачи оценки двух параметров
и
распределения
Вейбулла (табл. 1.1). Как следует из
табл.1.1, после приравнивания моментов
распределения ![]() и
и ![]() к
выборочным
к
выборочным ![]() и
и ![]() получается
система двух уравнений относительно
неизвестных оценок параметров
получается
система двух уравнений относительно
неизвестных оценок параметров ![]() и
и ![]() ,
аналитическое решение которой не
представляется возможным.
,
аналитическое решение которой не
представляется возможным.
Попытаемся подобрать
функциональное преобразование выборочных
значений ![]() ,
приводящее к упрощению поставленной
задачи оценивания. Заметим,
что двухпараметрический класс
вейбулловскихСВ Y может
быть получен с помощью нелинейного
преобразования
,
приводящее к упрощению поставленной
задачи оценивания. Заметим,
что двухпараметрический класс
вейбулловскихСВ Y может
быть получен с помощью нелинейного
преобразования ![]() СВ
с
экспоненциальным законом распределения:
СВ
с
экспоненциальным законом распределения: ![]() .
Такое преобразование упрощается, если
рассматривать прологарифмированные
данные эксперимента, т.е. ввести СВ
.
Такое преобразование упрощается, если
рассматривать прологарифмированные
данные эксперимента, т.е. ввести СВ ![]() и
соответствующие наблюдения
и
соответствующие наблюдения ![]() .
Но самое главное, что моменты
распределения
.
Но самое главное, что моменты
распределения ![]() оказываются
довольно простыми функциями неизвестных
параметров
и
.
Действительно,
оказываются
довольно простыми функциями неизвестных
параметров
и
.
Действительно,
![]() ;
;
![]() .
.
Используя таблицы интегралов [25], запишем:
![]() ,
,
![]() ,
,
где ![]() –
постоянная Эйлера [25]. С учетом приведенных
табличных интегралов получаем следующие
выражения для моментов распределения
логарифмов наблюдений:
–
постоянная Эйлера [25]. С учетом приведенных
табличных интегралов получаем следующие
выражения для моментов распределения
логарифмов наблюдений: ![]() .
.
Оценки 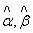 теперь
могут быть легко найдены из системы
двух уравнений
теперь
могут быть легко найдены из системы
двух уравнений ![]() ,
где
,
где 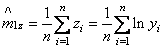 и
и ![]() –
выборочные моменты. После элементарных
преобразований решение системы уравнений
для оценок параметров распределения
Вейбулла запишется в виде:
–
выборочные моменты. После элементарных
преобразований решение системы уравнений
для оценок параметров распределения
Вейбулла запишется в виде:
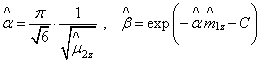 .
.
Полученные оценки могут использоваться, например, при построении классификатора типа помех в радиолокационном приемнике, поскольку распределение Вейбулла описывает широкий класс возможных помех в виде собственного шума приемника, отражений от местных предметов, гидрометеоров и др.
