45. Теорема Бернулли.

Рассмотрим схему Бернулли с вероятностью успеха   то есть пусть дана последовательностьнезависимых случайных величин   где

Определим   как число успехов в первых   испытаниях:

Тогда  при  то есть

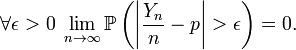
46 Выборка. Эмпирическая функция, полигон частот, гистограмма.

Выборка – совок-сть случайно отобранных объектов.

Объем выборки - число отобранных значений.

Генер. совок-сть – совок-сть объектов, из которых производится выборка.

При исследовании количественного или качественного признака СВ Х из общего числа возможных значений (генераль- ной совок-сти) извлекается случайным образом нек. число эл-тов. Эту совокупность элементов называют случайной выборкой или просто выборкой, а число n отобранных значений – объемом выборки.

Результаты всякого эксперимента запи- сывают в виде таблицы, в первой строке которой указывают номер эксперимента, а во второй – значение наблюдаемого признака Х, равное и называемое вариантой признака Х. Такая таблица наз. статистическим рядом. Статис-тический ряд, расположенный по воз-растанию вариант, наз. вариационным (x₁, x₂, …, x_n).

Если m_i – число наблюдений значения x_i признака Х, – общее число наблюдений (объем выборки), то число m_i / n наз. относительной частотой наблюдения x_i: .

Эмпирическая функция распределения выборки - функция , определяю-щая для всякого относительную частоту события , т.е. , где – число вариант, меньших x; n – объем выборки.

При больших объемах выборки интервал изменения всех ее вариант разбивают на определенное число интервалов равной длины, которые называются интервалами группировки. Затем подсчитывают число вариант выборки, попавших в каждый из интервалов, вычисляют относительные частоты числа вариант в каждом интервале.

Таблица, в которой дана система интер-валов, указаны частоты или относительные частоты числа вариант в каждом интервале, наз. статистической совокупностью.

Статистическую совокупность графически изображают с помощью гистограммы. Гистограмму строят следующим образом: по оси абсцисс откладывают интервалы, на каждом из них строят прямоугольники, площади которых равны частотам или относительным частотам попадания ва-риант в соответствующий интервал. Высо-ты этих прямоугольников равны  , или , где – длина выбранных интервалов. Полигоном частот наз. лома-ную линию, состоящую из отрезков, соеди-няющих точки

47. Числовые характеристики выборки.

Следующий этап обработки данных является вычисления числовых характеристик выборки. Главные из них: среднее значение, дисперсия, среднее квадратическое значение, моменты.  Так как функцию выборочных значений называют статистикой, то числовые характеристики, вычисленные по выборке, также называют статистиками.Числовые характеристики, вычисленные по генеральной совокупности, называют параметрами генеральной совокупности.

Для конкретной выборки объема n ее выборочное среднее   определяется соотношением: =, где хi – значение элемента выборки.  Обычно требуется описать статистические свойства произвольных случайных выборок одного объема, а не одной из них. Это значит, что рассматривается математическая модель, которая предполагает достаточно большое количество выборок объема n. В этом случае элементы выборки рассматриваются как независимые случайные величины Хi, принимающие значения хi с одной и тоже плотностью вероятностей f(x), являющейся плотностью вероятностей генеральной совокупности. Тогда выборочное среднее также является случайной величиной  , равной =.

По выборочным данным важно знать не только выборочное среднее, но и разброс выборочных значений около выборочного среднего. Если выборочное среднее является оценкой (приближенным значением) генерального среднего, то выборочная дисперсия должна быть оценкой генеральной дисперсии

Выборкой(выборочной совокупностью) называют совокупность объектов, отобранныхслучайным образом из генеральной совокупности. Если говорить более строго, то выборка– это последовательность независимых распре-деление каждой из которых совпадает с распределением генеральной совокупности.