1.Числ.Ряды.Необх.Признак сход-и.

Пусть дана числовая последовательность а1, а2, а3, +.., аn+ Выражение вида а1 + а2 + а3 +++ аn (1) - наз-ся числовым рядом Числа а1, а2, +, аn - наз-ся членами ряда. Числовой ряд (1) считается заданным, если извесен общий член ряда как функция an=f (n) Необходимый признак сходимости ряда.Теорема.Если ряд сходится, то un=0.

Доказательство. Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел . Тогда имеет место также равенство так как при n и (n-1) .Вычитая почленно из первого равенства второе, получаем - = = un=0, что и требовалось доказать.Следствие. Если un≠0, то ряд u1+u2+…+un… расходится.

2.Приз.сравнения рядов с полож.слаг.признак сравнения:

Рассмотрим два положительных числовых ряда и .. Если известно, что ряд – сходится, и выполнено неравенство (для ), то ряд тоже сходится.Иными словами: Из сходимости ряда с бОльшими членами следует сходимость ряда с меньшими членами. Предельный признак сравнения: Рассмотрим два положительных числовых ряда и . Если предел отношения общих членов этого ряда равен конечному, отличному от нуля числу то оба ряда сходятся или расходятся одновременно.

3.Признак Даламбера.

Пусть задана бесконечная последовательность чисел . Выражение u₁+u₂+…+u_n+…называется числовым рядом. При этом числа u₁, u₂, …, u_n… называются членами ряда. Числовой ряд часто записывают в виде .Теорема (необходимый признак сходимости ряда). Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n . Следствие. Если n-й член ряда не стремится к нулю при то ряд расходится. Теорема (признак Даламбера). Если в ряде с положительными членами u₁+u₂+…+u_n+…отношение n-го члена ряда к -му при имеет конечный предел D,т.е. 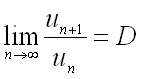то: - ряд сходится в случае Д<1.

4. Радикальный признак Коши.

Если для числового ряда с неотрицательными членами существует такое число , , что, начиная с некоторого номера, выполняется неравенство , то данный ряд сходится.

5. Интегральный признак Коши.

Интегральный признак Коши́ — признак сходимости убывающего положительного числового ряда. Признак Коши-Маклорена даёт возможность свести проверку сходимости ряда к проверке сходимости несобственного интеграла соответствующей функции на , последний часто может быть найден в явном виде.

Пусть для функции f(x) выполняется:

1. (функция принимает неотрицательные значения)

2. (функция монотонно убывает)

3. (соответствие функции ряду)

Тогда ряд и несобственный интеграл сходятся или расходятся одновременно.

6.Теор Признак Лейбница

Если у зн.ч. ряда n-й член стремится к 0 монотонно убывая, то ряд сх-ся, сумма ряда им. знак 1го члена ряда и не превосх. его по модулю.

 Пусть у зн.ч. ряда a1+a2-…-an+… lim |a_n|=0, |a1||a2||a3||an|=c_n тогда ряд запис. в виде с1-с2+с3-… (1), если a10 и –с1+с2-с3+… (2) если а10.

а10. Для частич. сумм с чёт. номерами n=2k имеем S_2k=c1-c2+c3-c4+…+c_2k-1-c_2k=

{(c1-c2)+(c3-c4)+…+ c_2k-1-c_2k (3)

{c1-(c2-c3)-(c4-c5)-…-c_2k (4). Т.к. с1с2…, то все скобки 0, поэтому (3) S_2k0, посл. {S_2k} возрастает: S_2k+2 = S_2k+ (c_2k+1-c_2k+2) S_2k. (4) S_2kc1. Т.о. {S_2k} возрастает и ограничена сверху она имеет конеч. lim S, причём 0 S_2kс10 Sс1.

Для посл-ти частич. сумм с неч. номерами n=2k имеем S_2k-1=c1-c2+…+c_2k-1=(c1-c2+…+c_2k-1-c_2k)+c_2k=S_2k+c_2k

lim(k) S_2k-1=(*по усл. lim(k) c_2k=0*)= lim(k) S_2k=S. Теперь покажем, что вся посл-ть {S_n} имеет предел S. Зададим >0. Тогда lim(k) S_2k=S(n1): (n=2kn1)[|S_n-S|<], а lim(k) S_2k-1=S(n2):(n=2k-1n2)[|S_n-S|<]. Возьмём n_=max{n1,n2}. Тогда (n> n_)[|S_n-S|<]. Это означ. Что lim S_n=S. Т.о. данный ряд сх-ся к сумме S, причём 0Sc1(*a10c1=a1*)0sa1. Ан-но в случае a10 док-ся, что ряд сх-ся к S, причём –с1S0(*а10-с1=а1*)а1S0. Т.о. S и а1 имеют один знак, причём |S||a1| 