Вопрос 11)Графики ф-ии бесселя,модифицированное уравнение Бесселя,графики модифицированных ф-ий Бесселя

Ряды для ф-й J_n (x) и Y_n (x) привод. в справ. лит-ре. Постр. гр-ки ф-и Бесселя и ф-и Неймана.

Грфики Бесселя(слева)-гладкие, непрерывные фии, ограничены в 0 и кбывают на∞.Фии Неймана неограниченно возрастает в 0, убывает на ∞

Ф-лы диффер. и инт. Бесселя.

Интегральные ряды для ф-и Бесселя

Инт-я ряды для ф Бесселя можно уст. ф-лу инт. для этих ф-й Ассимптотическое поведение ф-и Бесселя при больших аргументах.

Для оценки ф-и Бесселя при больш. арг. можно восп. ассимптотическимими ф-ми

Другие решения ур-я Бесселя.

Заметим что J_n(x) и Y_n(x) лин. незав. Поэтому ф-ции:

так же явл. лин независ. реш-ми ур. Беселя (ф-ции Ганкеля). Бывают удобными.

Запишем модифиц. ур-е Бесселя:

Оно получ из ур Бес подстановкой x=jx . значит его реш-ем явл ф-ция мнимого аргумента J_n ( jx) . На их основе строят лин независ модиф ф-и Бесселя 1 и 2 рода :

Общ-е реш-е предс-мо в виде: a , b = const (произвол.)

Гр-ки модиф-х ф-й.

Асимптотическое поведение ф Бесселя:

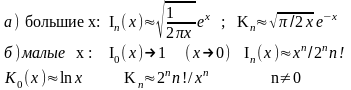
Вопрос 12)Ортогональность ф-ии Бесселя,ряд Фурье Бесселя

Ортогон-ть ф-и Бесселя. Р/м ур. Беселя (*)

Замена t = kx, приводит к стандартной ф.:

След-но. ф-и u (x) = J_n ( kx ) явл-ся решением ур-я (*) которое можно переписать в виде

умножая первое ур-ие на J_n(k₂x) а второе на J_n(k₁x) и вычитая 2-ое из первого получим

проинтегрируем это выражение по интервалу [0;l)

пусть теперь в этом соотношении к₁=M_i/l; k₂=M_j/l;

M_i и M_j корни ур-ия J_n(M)=0 Положим k₁= m_i /L ; k₂= m_j /L , m_i и m_j разл. корни ур-я

J_n(m)=0. j =/ i тогда из посл. соотн имеем усл. ортогон. ф-й Бесселя

₀^L xJ_n(k₁x)J_n(k₂x)dx = 0

₀ò^L xJ_n(xm_{i / L}) J_n(xm_{j / L})dx=0 i=\j

Говорят что ф-и Бесселя содержащие различные корни ур-я J_n явл. Ортогональными с весом x на отр.[0, L].Р-м случ i=j .В этом случ в (**) левя и прав часть Обращ в 0. Положим в этой ф. K₁= m _{/ L}

K₂-будем р/ать как перемен величину .Тогда из (**) имеем

₀ò^L xJ_n(xm _{/ L}) J_n(k₂x)dx=(mJ_n(k₂x)J_n^/ (m))/(k₂² – (m/L)²)

Устремим k₂ m/L и вычисл неопр (0\0) по пр.Лопиталя

₀ò^L xJ_n²(mx/L)dx=(L²/2)J_n^/(m)

Предыддущ утвержд сформ в теор об ортог Ф-и Бесс

Теорема:Если m₁ , m₂, m_k , явл корнями ур-я J_n(m)=0 или J_n^/ (m)=0, то sys ф-ций Бесселя : { J_n(xm_i / L)}

Явл ортогональной с весом x на [0.L] т.е. имеет место

Соотношение :

₀ò^L x J_n(xm_i /L) J_n(xm_j /L)x) dx = { 0 , i=/=j

{ (L²/2)J_n^/ (m) , i=j

( J_n (xm_i /L), J_n(xm_j /L) ) = {0, i=/=j

{ ||J_n ||²=(L²/2)J_n^{/ 2}(m) , i=j

Разложение в ряды по ф-м Бесселя.

Произв. ф-я f(x) на отр. [0;L] может быть прооксимир

Рядом Фурье по ф-циям Бесселя, т. е. предст. в виде :

Умножая слева и справа на J_n (xm_i /L) и интегрир от 0 до L получим значения С_k

Используя ортогон ф-й Бесселя, имеем:

Ряд апроксимирующий f(x) наз. рядом Фурье-Беселя.

Если f (x) непрерывна то ее ряд Ф-Б сх-ся абсолютно и равномерно. Если есть рарывы 1 рода – то ряд сх-ся среднеквадратично