Вопрос 9)Уравнение Эйлера, его базисные решения

Р/м ОДУ с перемен. коэф-тами 2^ого порадка специального вида, наиболее часто встречающиеся в мат.Физике: d²U/dt² + a₁(t) dU/dt + a₂(t) U=f (*)

a₁(t) и a₂(t) –известные ф-ции. Реш-е ищем на интервале [a; b], он может быть  или полубесконеч.

Справедливо утвержд: Если коэф-ты a_i непрерывны на [a ; b], то:

1) однородное ДУ (*) имеет два лин независ базисных решений (способы отыскания зависят от вида А_i-тых коэф-ов).

2) Общее реш. представимо в виде:

U(t) = C₁U₁(t)+C₂U₂(t)+U_f (t) где C₁ ,C₂ =const

U₁ ,U₂ –базис. реш-я ; U_f – ч. реш. (*). 3) Ч/реш может быть выражено через имп. реак U_f (t)=₀^t f()G(t-)d

Где G(t-)- имп. реакция сист описываемая ДУ (*)

4) имп. реакция отыскивается по такому же алгоритму как и ОДУ с постоян коэф-тами. Наиболее употребит в мат физике: Эйлера, Бесселя, модифицир ур-ния Бесселя, Лежандра, Присоединен ур-ние Лежандра

Ур-ния Эйлера. Общий вид:

a₀xⁿ y ⁽ⁿ⁾+a₁x ^n-1y ^(n-1)+a₂ x ^n-2y ^(n-2)+…+a_n-1 x y ^ʹ + a_ny=f

a_i – const . Переменные коэф-ты х. {e^t, x>0 }

Замена переменной: X= {-e^t, x<0}

Приведем к ДУ с постоянными коэф-тами, покажем это на примере ур-я Эйлера 2^ого порядка

a₀ x² yʹʹ+a₁x yʹ+a₂ y=0 пусть x>0; x=e^t ;

a₀(d²y/dt²) + (a₁-a₀)(dy/dt) + a₂y=0

Базисн. решение y=e^Pkt ; P_k –корни характ ур-я. a₀P²+(a₁-a₀)P+a²=0 Т.к. x=e^t, то можно записать базисное решение ур-ния Эйлера 2^ого порядка: y=x^Pk

В зависимости от вида решения характ. Ур-я возможны случаи: 1) Корни веществен и не равные P₁P₂ -> y_{1, 2} = x ^{P1, 2} . 2) Корни веществен и кратные P₁=P₂ -> y₁=x^P1 , y₂=x^P1 ln x . 3)Корни комплексные (нет новых базис реш, после выделения действит и мнимых частей приходим к первому случаю)

При реш неоднород ур-я Эйлера общее решение можно записать в виде: y(t)=C₁U₁(t)+C₂U₂(t)+U_f (t)

Где U_f можно выразить через имп. реакцию

Вопрос 10) Уравнение Бесселя, его базисные решения

Многие зад. МФ свод. к лин. ур-м Бесселя

(*)

- ур-е Бесселя порядка n.

В соотв. с общ. теор. лин. ДУ, реш. ур-я будем искать в виде ряда: 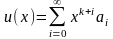(**) k-некот. параметр.

Подставляя предполаг. реш. (**) в (*) и вып. формальное диффер. Под знаком суммы получим (формальн.- т к мы не знаем сход или расх ряд U(x)).

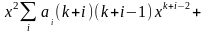
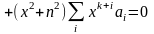
Степени х обр. лин. незав. Сист-му. Поэтому рав-во может быть реализов. лишь при рав-ве нулю коэф. при одинак степ х. Приравнивая эти коэф. 0 получим:

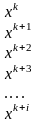
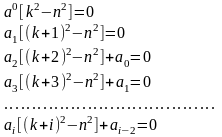
Будем искать реш. при а₀  0 в этом случае из 1-й стр. полу-чаем: k= n

Рассм. cлучай k=n, в этом случае из 2-й стр. стб. имеем

{ [ a₁ [ (n+1)² - n² ] ] , a₁=0 }

Из 4-й и посл-й стр-ки сл-ет что все посл. нечетн. коэф. будут равны 0, а все четн. коэф. выраж-ся через а₀ по ф-лам

а₀ – произв. а₂ = -а₀ / ( (k+2)² - n² )= -а₀ / ( 2² (n+1) )

а₄ = -а₂ / ( (k+4)² - n² ) = а₀ / ( 2⁴ (n+1)(n+2) * 1 * 2 )

a_2i = (-1) ⁱ * а₀ / ( 2²ⁱ (n+1) (n+2)*…*(n+i) *1*2*3*…*i )

При k= - n в этом выр-и вместо (n) нужно подставить (-n). Итак, k=n реш. (**) предст. в виде

Пользуясь произволом а₀ определим его как а₀ = 1 / ( 2ⁿ Г (n+1) ) где гамма ф-я опред. соотнош.

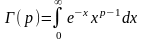
если вместо р положить целые числа n то инт. по частям легко получить: Г (n+1) = n!

Поэтому гамма-функция Г (р) - рассм-ся как расши- рение понятия фaктериала на целые зн-я аргумента

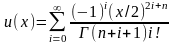
Анализ показывает что постр-я сумма на инт [ 0, ) абсол. и равномерно сход. , это значит что ф-я u (x) явл-ся одним из базисн-х реш-й ур-я Бесселя. Это реш ур-я Бесселя обознач. U (x) = J_n (x) и назыв-ся ф-ей Бесселя первого рода порядка n.

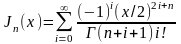
При k=-n имеем ф-ю Бесселя 1-го рода порядка (-n)

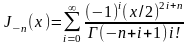
При дробн n т.е. ряд n J_n и J_-n лин-но незав. и явл-ся базисн. реш-м ур-я Бесселя, общ. реш. ур-я Бесселя представимо в виде: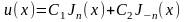

Легко проверить что при целых n имеет место соот-е:

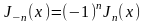
Это значит что эти ф-и лин. завис. и необх-мо постр. реш. Повторяя выкладки аналог. предъидущ. можно построить 2-е лин-но незав-е базисн-е реш-е ур-я Бесселя и наз. ф-й Неймана Y_n (x) . При целых n общ. реш-е ур-я Бесселя представ. в виде