Вопрос 53)Решение задачи Неймана методом гиу

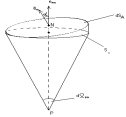. В этом случае в (**) функция dφ/dn известна, а φ(N) подлежит определению. Для ее описания перепишем (**) в виде (****) . . Интег-ное урав-ие 2^го рода решающ. З. Неймана. Общий вид ИУ 2^го рода: . K(M,N) - ядро ИУ, f(M) - свободный член, а φ(М)- искомая ф-ия, λ – пар-р. Это уравнение отличается от ИУ 1^го рода наличием неинтегрир. слагаемого φ(М). Это отличие существенно улучшает св-ва ИУ 2^го рода. Т.к. з. Неймана и (****) эквив-ы, то необх. и достат. условием разрешимости ИУ будет условие: . Известно что з. Неймана разрешима с точностью до конс-ты , это относится и к (****), для этого перепишем ядро ИУ в виде: . . Где dΩ_PN телесный угол под которым из т. Р видна площадка dS_N в окр-ти т. N. Используя все вычисления

Покажем что если φ – решение этого ИУ, то ф-ия φ(Р)+С - также решение. Достаточно пок-ть что С удовл. однор. ИУ. Подставим С в левую часть ИУ: . Следоват. любая конс-та С удовл. однород. ИУ, можно показать что других решений однородного ИУ не существует. Неедин-ть решения ИУ не позволяет численно решать это ИУ, поскольку Опред-ль соответств. СЛАУ будет близок к 0.

Вопрос 54)Теорема Фредгольма

Условие разрешимости ИУ 2^го рода ИУ, ядро которого удовлетворяет соотношению: называется ИУ Фредгольма (ИУ с квадратично интегрир. ядрами). Общий вид ИУ Фредгольма Значение λ, при котором однородное ИУФ 2^го рода имеет ненулевое решение, называется характеристич. значением ядра, а соответ-щее решен. – собственными ф-ями ядра. Веществ-ые ядра K(M,N) и K(N,M) называются сопряженными. Соответств. ИУ также называются сопряж-ыми. Основные св-ва ИУФ 2^го рода определ-ся теоремой Фредгольма об альтернативе. Теорема: Либо данная неоднородная ИУФ 2^го рода имеет решение и притом единственное при любой правой части f(P), либо соответственное однородное ИУФ имеет хотя бы одно ненулевое решение. Замеч. 1: записанная теорема справедлива не только для квадратично интегрир-ых ядер, но и для ядер со слабой особ-тью вида: , 0<α<mБ где G(M,N) непрер. ф-ия, а m – разм-ть области. Замеч. 2: Теорема Фредгольма может быть в виде: Либо λ не является характерист. значением для ядра и неоднор-ое ИУ имеет и при том единственное решение, либо λ – характерист. значение и ядро имеет хотя бы одну собственную функцию. Замеч. 3: возвращаясь к ИУ задач Дирихле и Неймана заметим что эти ИУ имеют ядра со слабой особенностью и поэтому на них распостраняется теория Фредгольма. Кроме того число λ=1/2π является характеристическим для ИУ (***) задачи Неймана и ему соответствует собственная функция φ=const