Вопрос 48) Метод Ритца

Вариационый принцип лежит в основе построения целого ряда численных схем решения краевых задач мат. физики. Рассм. в качестве примера решение з. Д. для ур. Л. на плоскости: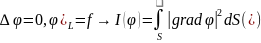 . Она эквивалентна минимизации. Приближен методы кот дают непосредственное реш зада-чи наз прямыми: методы Галёркина, каллокации, Ритца, наим квадр., метод конеч. элементов. Метод Ритца. Будем искать решение задачи (*) в виде комбинации нек системы ф-ций:  = f + c₁₁ + c₂₂ + ….+ c_n_n. (**) Здесь: f - произвол функция удовлетвор краевым услов. с_к – неизвес коэф-ты. _к- некоторые известные функции (наз. координатные). Необх подобрать с_к так чтобы minимизировать ф-ционал (*). Подставим (**) в (*): 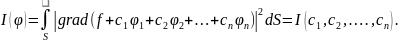Это ф-ция многих переменных С_К. Известно что необход. услов. для min функции многих переменных явл. 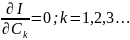Послед. ур-я задают СЛАУ относит Ск. Можно показать что необход услов. min явл. и достаточ. Запишем конкретный вид этой СЛАУ. Для этого введем: 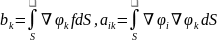. 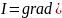Эти соотношения задают СЛАУ метода Ритца. Если в качестве коорд. ф-й выбрать систему лин. незав. функций то опред. СЛАУ (опред. Грамма) будет отличен от нуля и СЛАУ будет разрешима и притом единственным образом.После определения С_к Искомое решение: Замечание: 1. метод Ритца предполагает построение функционала соответствующего конкретной краевой задаче. 2: Успех применения метода Ритца зависит от удачного выбора координатных функций. Если выбраная коорд. функция хорошо апроксимирует искомое решение, то для решения необходимо взять их небольшое кол-во и тогда СЛАУ будет иметь небольшой порядок.

Вопрос 49)Методы взвешенных невязок,метод коллокации

Эти м. представляют собой численные процедуры построения приб-ых реш-й краевых задач для ур-ий МФ. Р/м идею метода на примере реш. плоской задачи Дирихле для ур-я Пуассона. Приб-ое реш-е этой задачи будем искать в виде.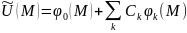 . Где ₀-произвольная функция удовл-щая граничным условиям задачи. _К-известные функции с однор. гранич. услов.(лин не зависимая система ф-ций), С_к-искомые коэф. Подставляя (*) в урав задачи получим невязку решения. . При численном решении задачи стараются невязку сде-лать =0 в среднем приравнивая к нулю интегралы от невязки с некоторыми весовыми ф-циями.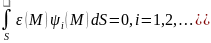 . Здесь _i-весовые функции. В зависимости от выбора весовых ф-й получ. разл. варианты метода взвеш. невязок: метод коллокации, наим квадратов, Галёркина.

Метод коллокации. В этом методе в качестве весовых ф-й _i используется дельта ф-я. _i (M) = ( M-M_i ). Свойства: . Подставляя это в (**) и используя свойства получим. 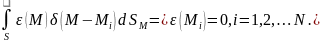В этом методе невязка точно=0 в конечном числе точек M_i (точек каллокации).Подст-я вместо невязки конкретное знач-е пол-м СЛАУ: . Зам-м что в м. коллокации баз-е ф-ии в нач-ом приб-и U₀ должны быть 2-ы дифуемы. Зам-ие: Если число точек каллокации M_i больше числа базисных ф-й  _К то СЛАУ несовместна и можно найти  в некотор. смысле реш-е. Это можно сделать методом наим. квадр.